강의 링크 : https://www.boostcourse.org/ai100/lecture/739176?isDesc=false

벡터

• 숫자를 원소로 가지는 리스트 또는 배열
• 숫자(원소)의 개수가 벡터의 차원이 된다.
• 파이썬에서는 벡터를 다룰 때 주로 numpy의 array를 사용한다. ※ 내장 모듈이 아니므로 pip나 conda를 통해 numpy 패키지를 설치해야한다.

import numpy as np
x = np.array([1, 2, 3])

• 벡터의 성분을 세로로 나열하면 열벡터라 하고, 가로로 나열하면 행벡터라 한다.

• 벡터는 공간에서 원점으로부터의 상대적 위치를 한 점으로 나타낸다.

  • 그림으로 나타낼 수 있는 점은 3차원까지지만, 벡터는 보통 그보다 큰 n차원을 다룬다.
  • 하지만 n차원 공간의 한 점을 표현한다는 것은 동일하다.

스칼라곱

• 벡터에 숫자를 곱해주면 벡터의 길이만 변화하는데, 이를 스칼라 곱이라 한다.
• 스칼라곱이 1보다 크면 길이는 증가하고, 1보다 작으면 감소한다.
• 음수를 곱할 경우 방향이 반대가 된다.

벡터의 연산

• 벡터간의 연산을 위해서는 일반적으로 같은 모양(같은 차수)이어야 한다.
  • numpy에서 차원이 다른 두 벡터를 연산하면 에러가 출력된다.
  • 즉 벡터에서 차원의 개수는 매우 중요하다.
• 벡터간의 덧셈, 뺄셈 계산이 가능하다.
• 벡터간의 곱셈은 여러가지 종류가 있는데, numpy에서 곱하기 기호(*)를 사용하면 성분곱(Hadamard product 또는 Element wise product)을 구한다.
  • 성분곱은 같은 차원의 원소를 서로 곱한 것이다.

x = np.array([1, 2, 3])
y = np.array([5, 2, 1])
x + y # array([6, 4, 4])
x - y # array([-4, 0, 2])
x * y # array([5, 4, 3])

벡터의 덧셈

• 두 벡터의 덧셈은 다른 벡터로부터 상대적인 위치이동을 표현한 것이다.
  • 원점을 0이라 할 경우 x = 0 + x가 성립한다.
  • x + y의 경우 x를 원점으로한 y벡터와 같다. (반대도 성립)

벡터의 뺄셈

• 두 벡터의 뺄셈은 방향을 뒤집은 덧셈과 같다.
  • y - x의 경우 y를 원점으로 표현한 x 벡터와 같다.

벡터의 노름(norm)

• 벡터의 노름은 원점에서부터의 거리를 말한다.
• 벡터에는 여러가지의 노름이 존재하는데, 벡터의 차원과 상관없이 수많은 노름을 구할 수 있다.

• 벡터 x의 노름은

  x

  로 나타낸다.

L1 norm

• 벡터의 성분의 절대값 합과 같다.
• 각 성분의 변화량의 절대값을 의미한다. (좌표축을 따라 점까지 이동한 거리)

• x

  1로 나타낼 수 있다.

x = np.array([1, 3, 6])
x_norm1 = np.abs(x)
x_norm1 = np.sum(x_norm1) # 10

L2 norm

• 벡터 성분의 제곱합을 제곱근 한것과 같다.
• 피타고라스 정리를 이용해 유클리드 거리를 계산한 것과 같다.

• x

  2로 나타낼 수 있다.

x = np.array([3, 4])
x_norm2 = x * x
x_norm2 = np.sum(x_norm2) # 25
x_norm2 = np.sqrt(x_norm2) # 5

다른 노름을 사용하는 이유

• 노름의 종류에 따라 기하학적 성질이 달라진다.
  • 원을 나타내는 [1, 0], [0, -1], [-1, 0], [0,1]의 경우
  • L1 노름으로 나타내면 마름모가 된다.
  • L2 노름으로 나타내면 원이 된다.
• 머신러닝에서는 데이터의 특성과 목적에 따라 다른 성질이 필요하므로 목적에 맞게 서로 다른 노름을 사용한다.

두 벡터 사이의 거리

• 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈을 이용하면 된다.
  • x와 y사이의 거리는 x-y 또는 y-x와 원점 사이의 거리와 같다.

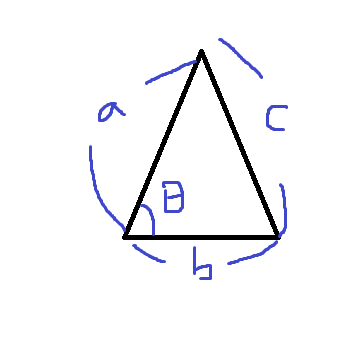
두 벡터 사이의 각도

• 두 벡터 사이의 각도를 구하기 위해서는 L2-노름을 사용해야 한다.
• 내적과 코사인 제 2법칙을 이용하는 것을 통해 두 벡터 사이의 각도를 계산할 수 있다.

제2 코사인 법칙 : a² = b² + c² - 2bc * cos θ

• L2-노름은 유클리드 거리를 나타내므로 다음과 같이 나타낼 수 있다.

cos θ = (

x

22 +

y

22 -

x-y

22) / (2 *

x

2 *

y

2)

내적 (inner product)

• 내적은 두 벡터의 성분곱을 취한 것의 성분합과 같다.
• 내적은 <x, y>로 나타낼 수 있다.
• numpy 에서는 inner() 함수로 쉽게 내적을 구할 수 있다.

cos θ = <x, y> / (

x

2 *

y

2 )

파이썬에서 두 벡터의 각도 구하기

def angle(x, y):
	cos_theta = np.inner(x, y) / (norm_2(x) * norm_2(y)) # cos θ
    theta = np.arccos(cos_theta) # arccos는 아크코사인 값을 구하는 함수
    return theta

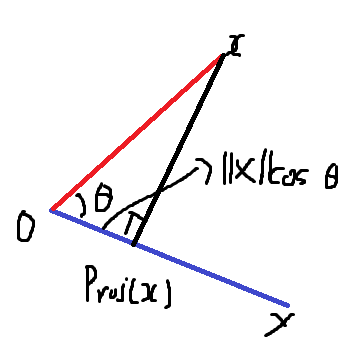
내적의 해석

• 내적은 정사영(orthgonal projection)된 벡터의 길이와 관련이 있다.

정사영의 간단한 정의는… 나무위키 링크

• x벡터와 y벡터에서, Proj(x)는 벡터 y로 정사영된 벡터 x의 그림자를 말한다.
• 이때 Proj(x)와 x를 잇는 선분을 그리면 직각삼각형이 완성되는데, 여기서 Proj(x)의 길이는 코사인법칙에 의해 ||x||cos θ가 된다.

• Proj(x)에 ||y||를 곱하면 내적이 된다.

<x, y> =

x

2

y

2cos θ =

y

Proj(x)

• 여기서 ||y||는 Proj(x)의 스칼라곱과 같으므로, 내적은 정사영의 길이를 벡터 y의 길이만큼 조정한 값이라 할 수 있다.
• 때문에 내적은 두 벡터의 유사도(similarity)를 측정하는데 사용할 수 있다.