Post

Posted Updated
By Changjin Kang
views 8 min read

참고하면 좋은 글 들

문제 : 2623. 음악프로그램

  • 위상 정렬 알고리즘 문제인 백준 음악프로그램문제를 통해 위상 정렬 알고리즘을 알아보자.

위상 정렬 알고리즘

위상 정렬이란

  • 위상 정렬 알고리즘은 단방향 그래프에서 기존의 방향(순서)를 거스르지 않고 노드를 나열하는 알고리즘이다.

  • 일렬로 나열한다는 것은 무슨뜻일까?

img

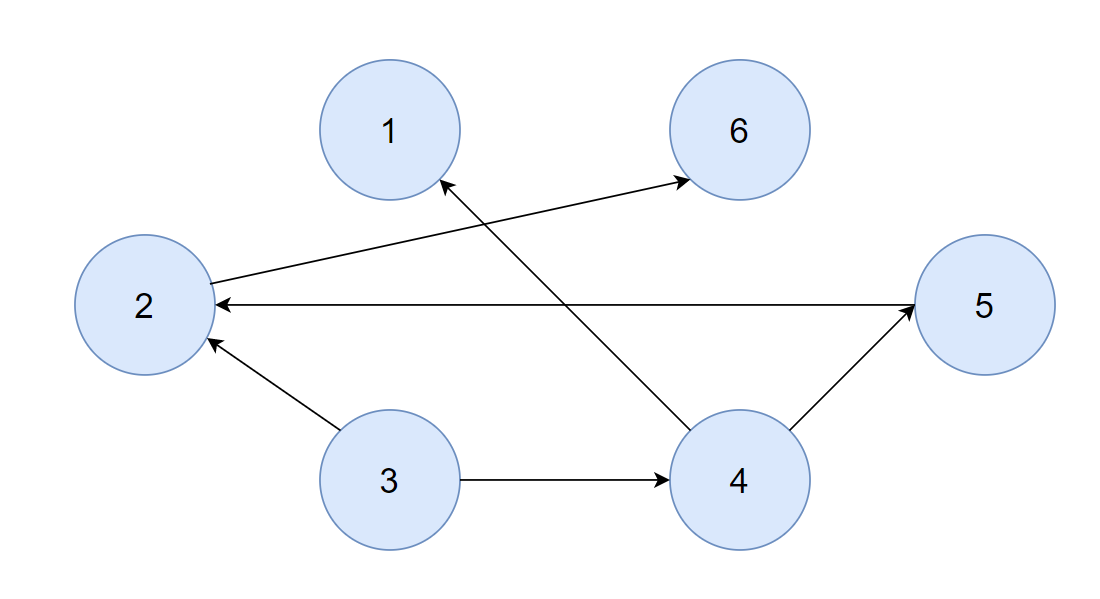
  • 이런 단방향 그래프가 주어졌다고 가정했을 때, 노드의 위치만 바꾸면 다음과 같이 그릴 수 있다.

img

  • 위와 같이 일렬로 정렬할 수 있으며, 정렬된 그래프의 간선이 모두 같은 방향을 가리키는 것을 알 수 있다.
  • 이렇게 모든 간선의 방향이 유지되면서 일렬로 나열되는 경우를 위상 정렬되었다고 할 수 있다.
  • [1, 6, 2, 5, 4, 3]은 위상 정렬된 배열이다.

img

  • 만약 1과 4의 위치가 바뀐다면 방향이 다른 간선이 발생하기 때문에 정렬되었다고 볼 수 없다.
  • [4, 6, 2, 5, 1, 3]은 위상 정렬되지 않은 배열이다.

위상 정렬이 불가능한 경우

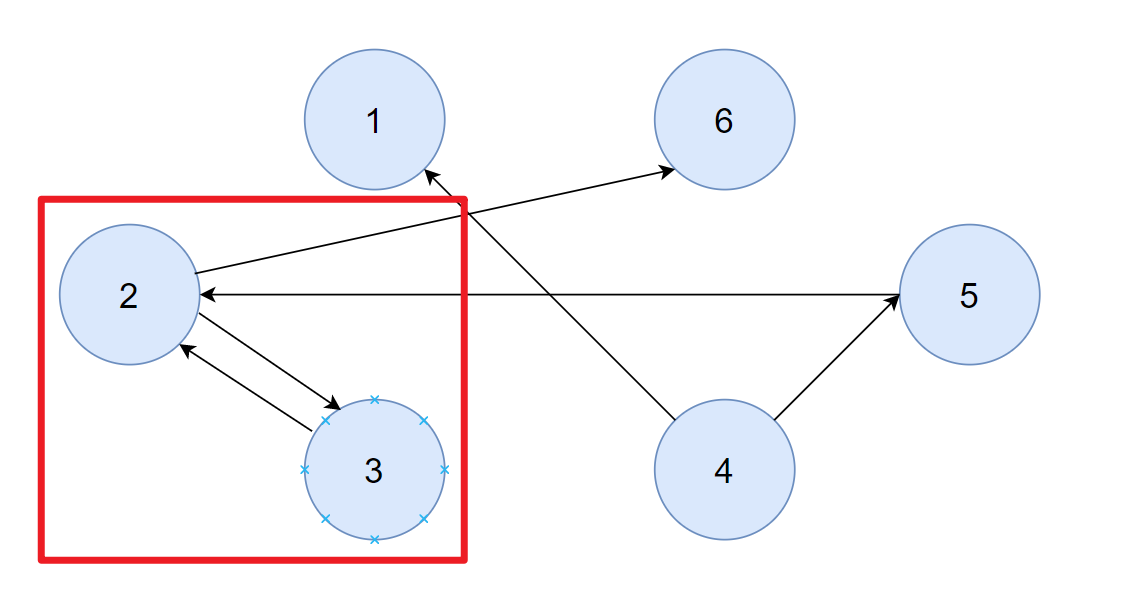
  • 그래프에 사이클이 존재할 경우 위상 정렬이 불가능하다.

img

imgimg

  • 위 그림과 같이 어떻게 배열을 해도 위상 정렬이 되지 않게 된다.

위상 정렬 알고리즘 구현

  • 위상 정렬을 위해서는 각 노드별로 두 개의 정보가 필요하다.
    • a. 내가 가리키고 있는 노드의 수 (나보다 먼저 나열되어야 할 노드 수)
    • b. 나를 가리키고 있는 노드 (내 뒤에 나열되어야 할 노드)
  • 추가로 정렬된 결과를 저장할 리스트 c가 있다고 하자.

필요한 데이터 정의

  • 첫번째 예시는 다음과 같이 표현할 수 있다.

img

 123456
a012210
b[4][3, 5][ ][3][4][2]
  • 예시
    • 4번 노드는 1, 5 두 개의 노드를 가리키고 있어 a[4] = 2이며 3이 자신을 가리키고 있으므로 b[4] = [3]이다.
    • 2번 노드는 6 하나를 가리키고 있어 a[2] = 1이며 3, 5가 자신을 가리키고 있으므로 b[2] = [3, 5]이다.

a[i] = 0인 노드 찾기

  • a[i] = 0이라는 것은 나보다 먼저 정렬되어야 할 노드가 하나도 남지 않은 것을 의미한다. 즉 내가 정렬되면 된다.

  • 여기서는 큐를 이용하여 노드를 저장한다.

    • que = [1, 6]

a[i] = 0인 노드 정렬하기 및 다음 노드 찾기

  • 이제 큐에서 값을 하나씩 빼주면서(leftpop) 정렬을 진행한다.

  • 다음은 b[i]를 이용해 a를 업데이트한다.
    • 예를들어 6번 노드를 꺼냈다면 b[6]에 저장된 노드들은 자신이 기다려야 할 노드가 하나 줄었다는 것이다.
    • 6을 꺼내어 정렬했을 때 b[6] = [2]이므로 a[2]의 값을 하나 빼주면 된다.
    • 이 때 a[2] - 1 = 0이 되므로 정렬될수 있는 새로운 노드가 생겼다. 2를 큐에 append하면 된다.
  • 결과적으로 a[i] = 0을 만족하는 1, 6을 정렬하면 다음과 같이 업데이트 된다.

||1|2|3|4|5|6| |:—:|:—:|:—:|:—:|:—:|:—:|:—:| |a|0|0|2|1|1|0| |b|[4]|[3, 5]|[ ]|[3]|[4]|[2]| c = [1, 6] que = [2]

  • 이어서 BFS를 돌면서 큐가 빌 때까지 반복하면 된다.

||1|2|3|4|5|6| |:—:|:—:|:—:|:—:|:—:|:—:|:—:| |a|0|0|1|1|0|0| |b|[4]|[3, 5]|[ ]|[3]|[4]|[2]| c = [1, 6, 2] que = [5]

||1|2|3|4|5|6| |:—:|:—:|:—:|:—:|:—:|:—:|:—:| |a|0|0|1|0|0|0| |b|[4]|[3, 5]|[ ]|[3]|[4]|[2]| c = [1, 6, 2, 5] que = [4]

||1|2|3|4|5|6| |:—:|:—:|:—:|:—:|:—:|:—:|:—:| |a|0|0|0|0|0|0| |b|[4]|[3, 5]|[ ]|[3]|[4]|[2]| c = [1, 6, 2, 5, 4] que = [3]

||1|2|3|4|5|6| |:—:|:—:|:—:|:—:|:—:|:—:|:—:| |a|0|0|0|0|0|0| |b|[4]|[3, 5]|[ ]|[3]|[4]|[2]| c = [1, 6, 2, 5, 4, 3] que = [] —> 반복 종료

  • 결과적으로 c = [1, 6, 2, 5, 4, 3]의 위상 정렬된 리스트를 얻을 수 있다.

2623. 음악프로그램

1
2
3
4
5

예제
6 3
3 1 4 3
4 6 2 5 4
2 2 3

  • 사실 음악프로그램에 있는 문제가 바로 위에서 풀었던 예제이다.

  • 먼저 출연해야 하는 가수가 먼저 정렬되어야 하는 노드와 같다.

  • 정렬이 불가능한 경우는 위상 정렬 알고리즘을 모두 수행한 결과(리스트)의 길이가 출연 가수의 수(N)보다 작은 경우이다.

    • 정석은 사이클 여부를 확인하는 것이지만 음악프로그램 문제에서는 이 방법이 편하다.

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

import sys
from collections import deque

input = sys.stdin.readline

N, M = map(int, input().split())

# 자신보다 먼저 불러야하는 가수의 수 (위상정렬)
a = [0] * (N+1)
a[0] = -1
# 자신 뒤에 불러야하는 가수를 저장하는 배열
b = [[] for _ in range(N+1)]
for _ in range(M):
    temp = list(map(int, input().split()))
    length = temp[0]
    # 먼저 불러야하는 사람 수, 뒷 순서로 불러야할 사람 업데이트
    # 첫번째 부르는 사람은 앞사람이 없으므로 두번째부터 시작
    for i in range(2, length+1):
        prev_s = temp[i-1]
        s = temp[i]
        a[s] += 1
        b[prev_s].append(s)
# 위상정렬 위해 큐 초기화
que = deque()
for idx, num in enumerate(num_prev):
    if not num:
        que.append(idx)
# 위상정렬
c = []
while que:
    s = que.popleft()
    for s_next in b[s]:
        a[s_next] -= 1
        # 자신 앞에 부를 사람이 없게되면 큐에 추가
        if not a[s_next]:
            que.append(s_next)
    # 정렬
    c.append(s)

# 모든 가수가 노래를 부를 수 있는 경우 순서대로 출력, 아니면 0 출력
if len(answer) == N:
   [print(s) for s in answer]
else:
    print(0)
This post is licensed under CC BY 4.0 by the author.