문제 : https://www.acmicpc.net/problem/9663

N * N 크기의 체스판이 주어지면 N개의 퀸이 서로 공격할 수 없도록 배치하는 문제이다.

문제 요약

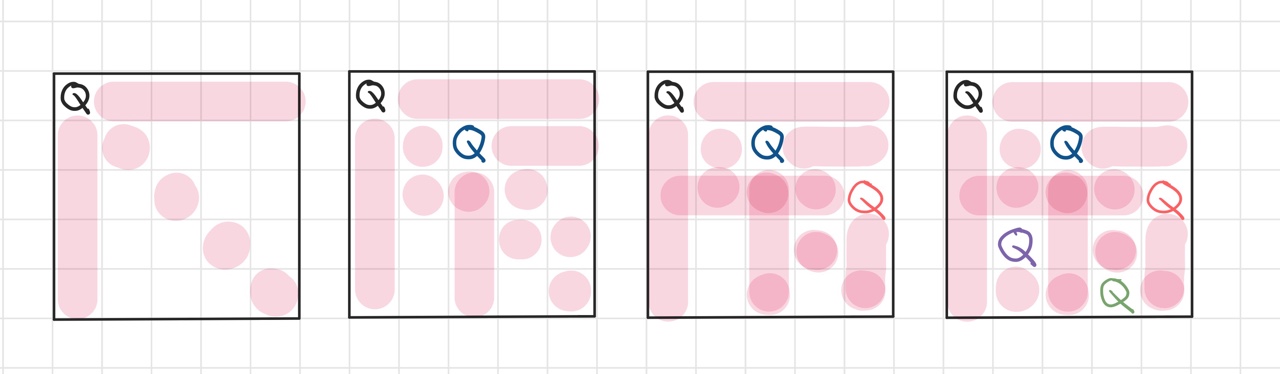
위 그림과 같이 5 * 5 행렬이라면 퀸이 서로 공격할 수 없게 5개의 퀸을 배치할 수 있다.

풀이

브루트 포스

기본적으로 이 문제는 퀸을 놓을 수 있는 모든 경우의 수를 따져봐야한다.

그러나 이 문제에서 주어진 N의 범위는 최대 15로, N*N 행렬을 정직하게 탐색한다면, 탐색만 해도 약 (15*15)^15번의 탐색을 해야한다.

때문에 퀸을 어떤 경우에 놓을 있는지 따져야 한다.

1. 같은 행에는 다른 퀸이 있을 수 없다.
2. 같은 열에는 다른 퀸이 있을 수 없다.
3. 대각선에는 다른 퀸이 있을 수 없다.

여기서 알 수 있는 것은 어짜피 N행에 N개의 퀸을 놓을려면 결국 한 행에 하나의 퀸만 놓을 수 있다는 것이다.

즉 0번부터 시작해서 N-1까지 순차적으로 for loop을 돌면서 열 만탐색해도 브루트 포스를 구현할 수 있다.

이를 위한 자료구조는 다음과 같다.

1. [0, -1, -1, -1, -1]
2. [0, 2, -1, -1, -1]
3. [0, 2, 4, -1, -1]
4. [0, 2, 4, 1, -1]
5. [0, 2, 4, 1, 3]

이렇게 N*N 행렬을 만들지 않아도 i번째 인덱스의 값 j를 통해 i행 j열에 퀸이 있다는 것을 나타낼 수 있다.

자연스럽게 0 ~ i-1 행까지의 값을 탐색하면 j열에 다른 퀸이 없다는 것도 알아낼 수 있다.

대각선 퀸 여부 확인하기

다음으로 알아야 할 것은 내가 퀸을 놓고자 하는 자리의 대각선 상에 다른 퀸이 있는지 알아야 한다.

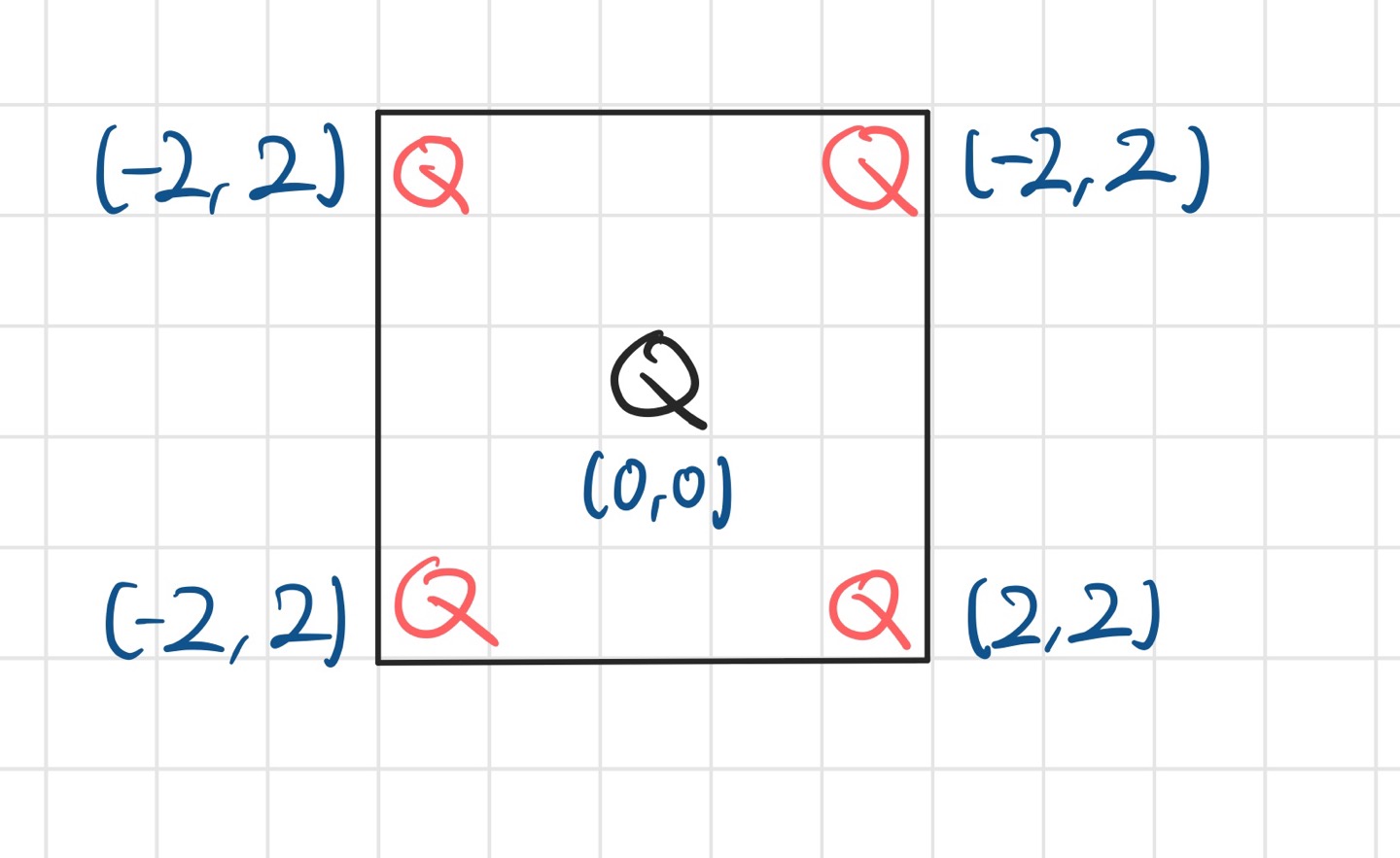
기준이 되는 퀸은 검은색, 대각선에 존재할 수 있는 퀸을 빨간색으로 표시하였다.

그림을 보면 기준점으로부터 x, y의 절대값이 같다는 공통점을 확인할 수 있다. 즉, x' - x == y' - y 조건을 만족하면 (x, y)의 퀸과 (x’, y’)의 퀸은 대각선 상에 있다고 할 수 있다.

이를 코드로 나타내면 다음과 같다.

def is_queen(x):
    # 이전 행에 놓였던 퀸에 대해 탐색
    for xx in range(x):
        # 이전 행에 놓인 퀸과 같은 열이거나, 대각선에 있을 경우 놓을 수 없음
        if board[x] == board[xx] or abs(board[x]-board[xx]) == abs(x-xx):
            return False
    return True

자신의 이전행에 있는 모든 퀸에 대해 같은 열에 있는지, 대각선 상에 있는지를 체크한다.

정리

결론적으로 풀이 과정은 다음과 같다.

1. 0 ~ N-1 까지 N회 재귀하도록 행 번호를 하나씩 늘려가면서 재귀적 호출
2. 각 i번째 재귀 함수에서는 0 ~ N-1까지 열번호를 하나씩 늘려가면서 퀸을 놓을 수 있는 자리인지 판별하는 함수(is_queen 호출)
3. is_queen에서는 0 ~ i-1행까지 퀸이 같은 열에 있는지, 대각선에 있는지 확인한 후, 있다면 False, 없다면 True를 반환

코드

# 현재 칸에 퀸을 놓을 수 있는지 판별하는 함수
# x: 판별할 칸의 행 좌표
def is_queen(x):
    # 이전 행에 놓였던 퀸에 대해 탐색
    for xx in range(x):
        # 이전 행에 놓인 퀸과 같은 열이거나, 대각선에 있을 경우 놓을 수 없음
        if board[x] == board[xx] or abs(board[x]-board[xx]) == abs(x-xx):
            return False
    return True
    
# 퀸을 놓을 수 있는 칸에 퀸을 놓는 함수
# i: 현재 보드에 놓인 퀸의 개수(이번에 놓아야할 퀸의 행 번호)
def put_queen(i):
    global answer
    # 보드에 퀸이 N개만큼 놓이면 방법의 수를 1증가 시킴
    if i == N:
        answer += 1
        return

    for j in range(N):
        board[i] = j
        if is_queen(i):
            put_queen(i+1)

if __name__=="__main__":
    N = int(input())
    answer = 0
    # 배열 초기화
    board = [-1] * N
    
    # 무조건 한 줄에 하나씩 있을 수 있으므로 각 줄을 탐색하면 됨
    put_queen(0)
    
    print(answer)

소감

사실 풀이법은 맞았는데, 변수 선언위치 등 최적화에 따라 시간초과가 되냐 마냐가 갈리는 까다로운 문제라 많이 헤맸다.

브루트포스 문제를 풀때마다 느끼는 것인데 이럴때는 파이썬이 정말 불리한 것 같다…