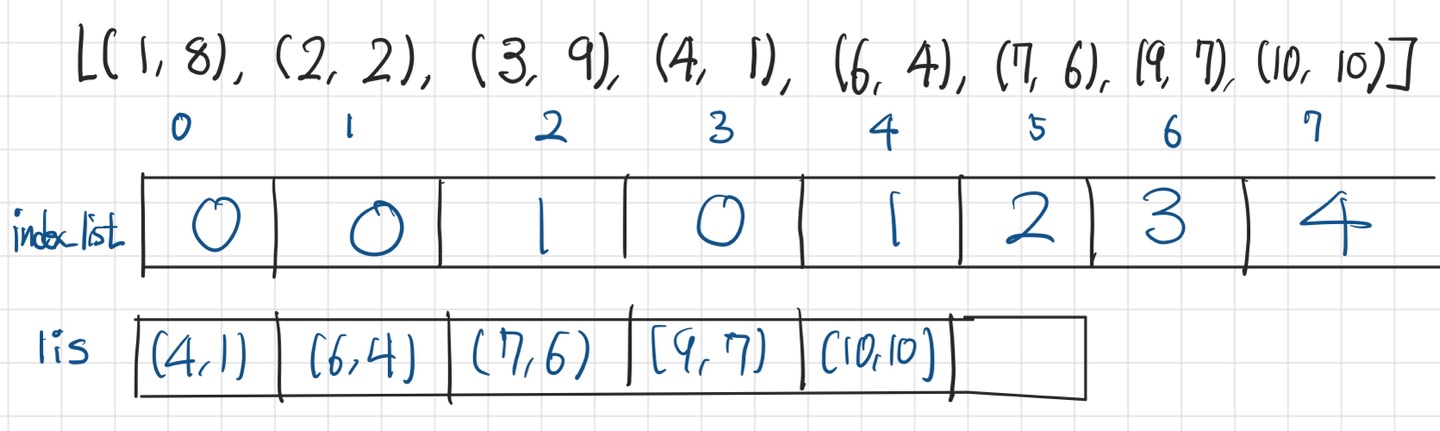문제 : https://www.acmicpc.net/problem/2568
문제 요약
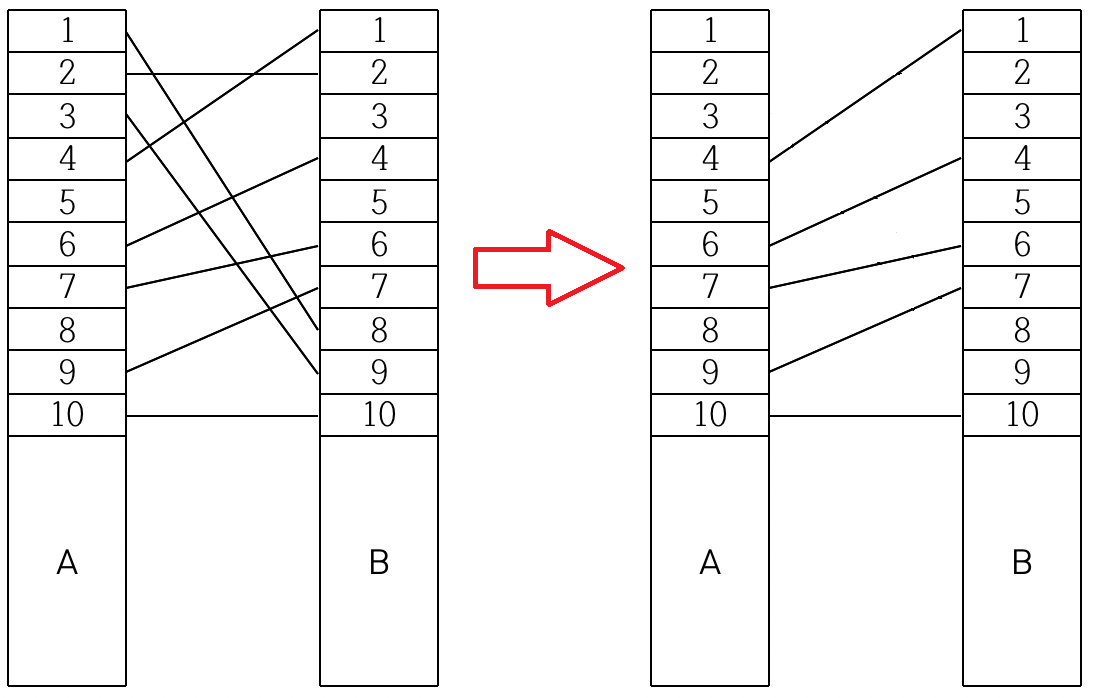
위와 같이 전봇대 A와 B 사이에 연결된 전깃줄을 모두 꼬이지 않게하면서 최소한으로 제거하는 방법을 찾는 문제이다.
이 문제의 난관은 제거해야하는 전깃줄을 오름차순으로 출력해야한다는 것이다. 위의 경우 [1, 2, 3] 총 3개를 제거한 것이며, [1, 3, 4] 3개를 제거하는 것도 답이 될 수 있다.
결론부터 말하자면 이 문제는 ‘가장 긴 증가하는 부분 수열(LIS)’의 심화문제라고 할 수 있다.
풀이
1. A와 B 중 하나를 정렬하기
제거된 전깃줄을 보면 (4, 1), (6, 4), (7, 6), (9, 7), (10, 10)으로 A를 기준으로 보나 B를 기준으로 보나 모두 오름차순 정렬되어있다는 것을 확인할 수 있다.
즉, A나 B 중 하나를 오름차순 정렬한 뒤에 이를 기준으로 나머지의 가장 긴 증가하는 부분 수열(LIS)을 구하면 가장 많은 전깃줄을 꼬이지 않게 연결할 수 있다.
A, B 순으로 각각 입력되므로 A를 기준으로 정렬하였다.
1
2
3
# A를 기준으로 정렬
arr = [tuple(map(int, input().split())) for _ in range(N)]
arr.sort(key = lambda x : x[0])
2. LIS의 길이 및 LIS의 마지막 인덱스 구하기
완전 탐색이라면 O(N^2)의 시간복잡도이지만, 이분 탐색을 통해 LIS의 길이와 LIS의 마지막 인덱스를 구할 수 있다.
이거는 직접 설명하면 풀이가 너무 길어질 것 같아 다른 분들이 잘 설명한 자료를 참고하면 좋을 것 같다.
위 내용을 이해하고 있다는 가정을 하에 나머지 과정을 작성하겠다.
이 문제에서 차이점이 있다면, 이분 탐색을 통해 길이를 구하는 과정에서 로깅을 해야한다는 것이다.
과정을 설명하면 다음과 같다.
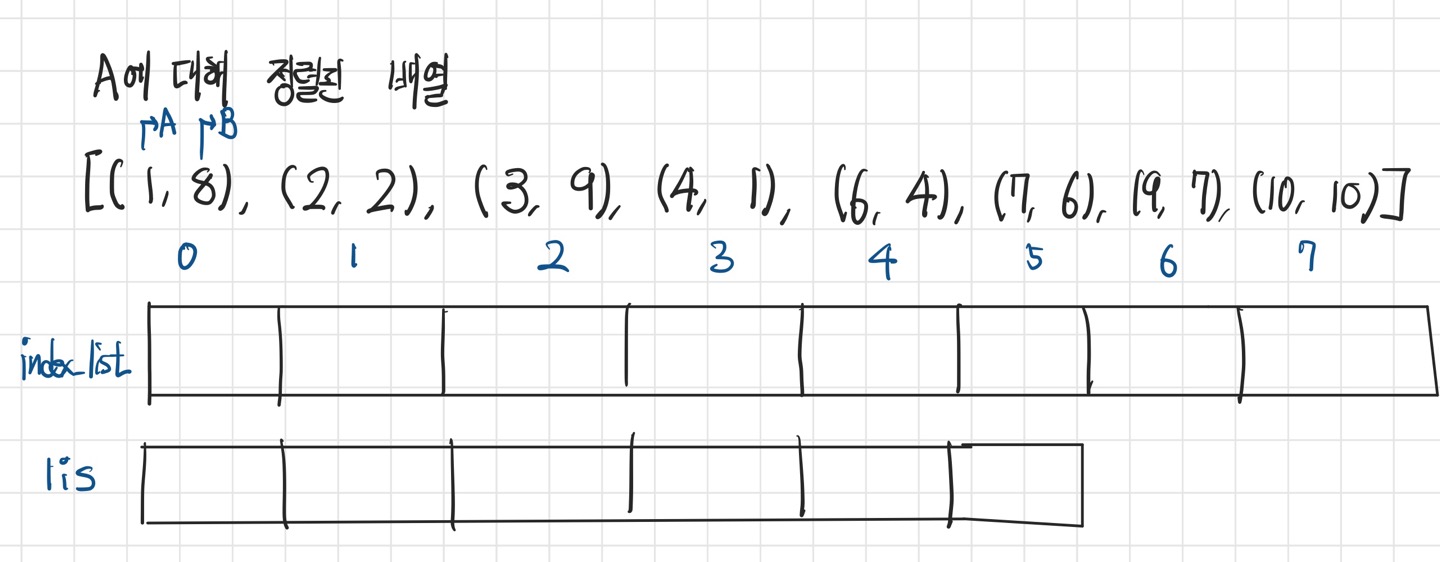
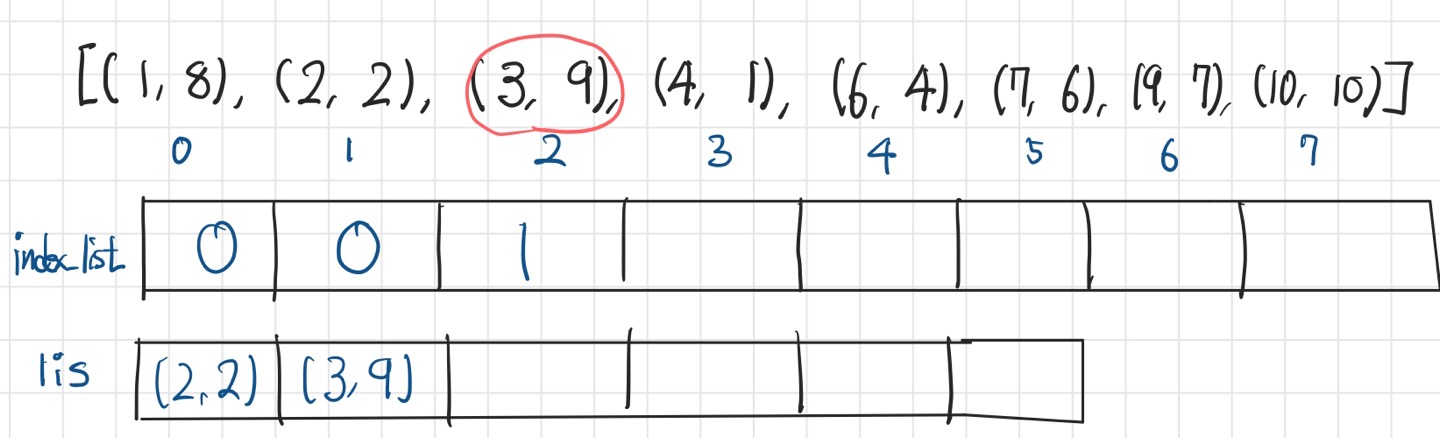
1. 증가수열을 저장할 리스트(lis)와 로깅할 리스트(index_list)를 초기화한다.
- lis는 빈 배열을 선언
- index_list는 전깃줄 배열의 크기 N과 동일하고 1:1로 매핑된다.
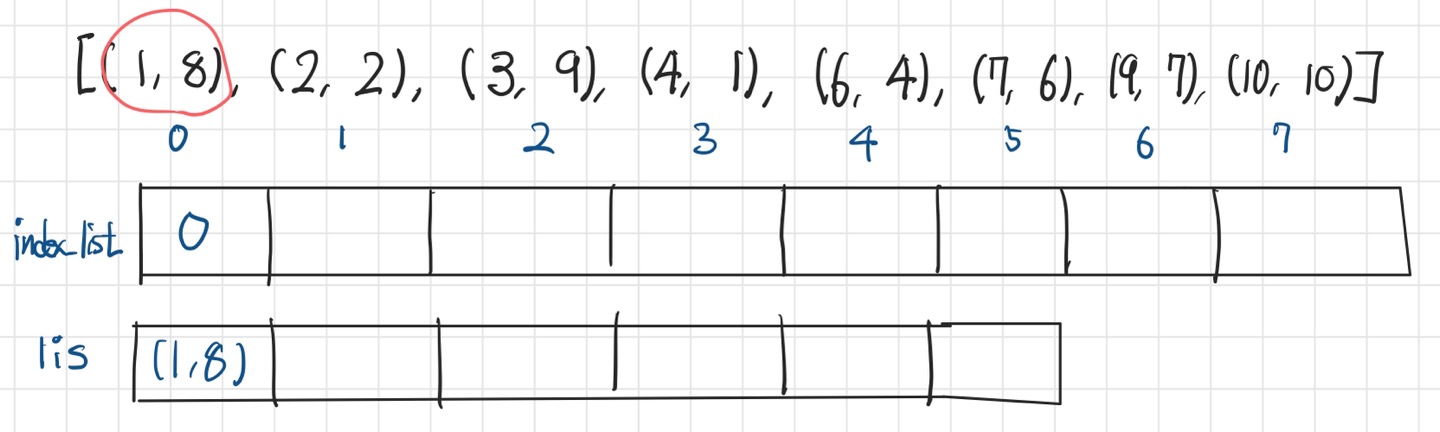
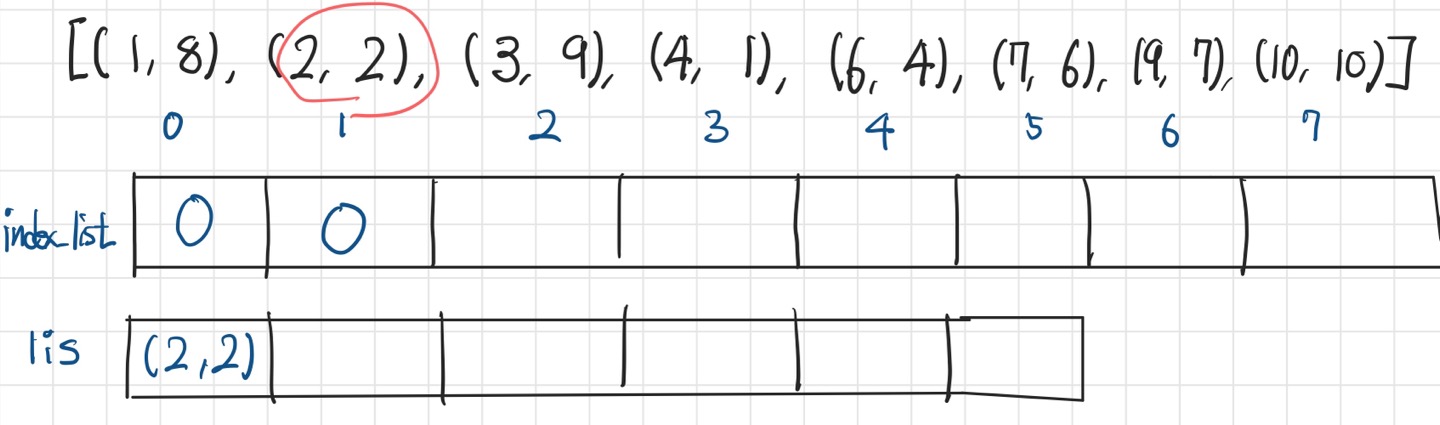
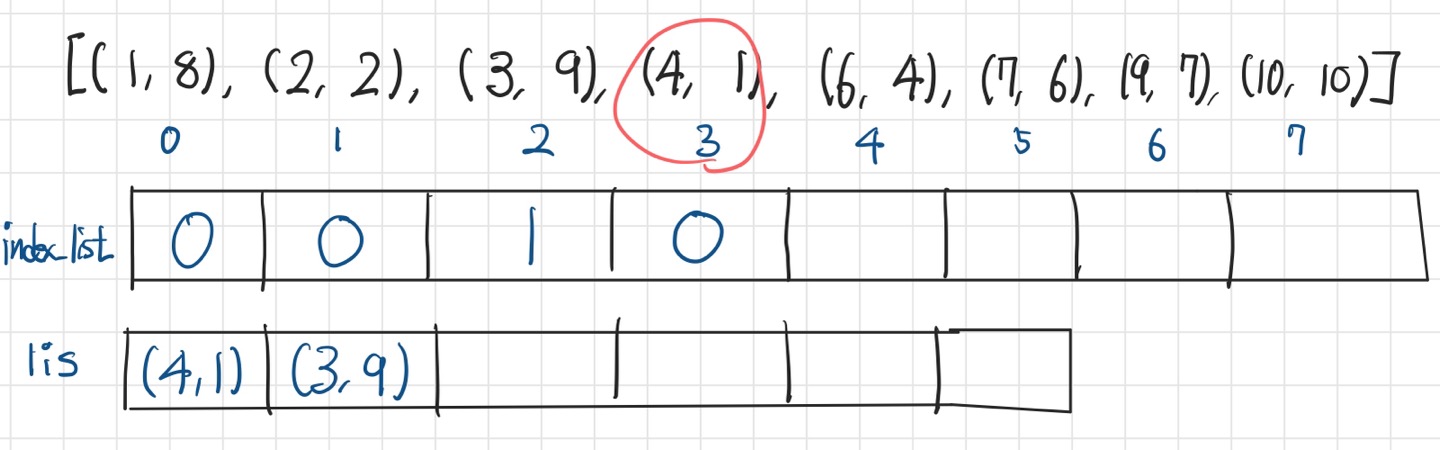
2. index_list에는 전깃줄 정보가 lis 배열의 몇번 인덱스에 저장되었는지를 로깅한다.
동일과정을 반복하면 최종적으로 위와 같이 된다.
현재 구해진 lis는 실제 lis가 아니라, 실제 lis의 길이와 마지막 값이 무엇인지만 알 수 있는 상태이다. 위 예제에서 lis의 길이는 5이며, 마지막으로 (10, 10)을 갖는다는 것을 알 수 있다.
3. index_list를 기준으로 역탐색하며 실제 lis 구하기
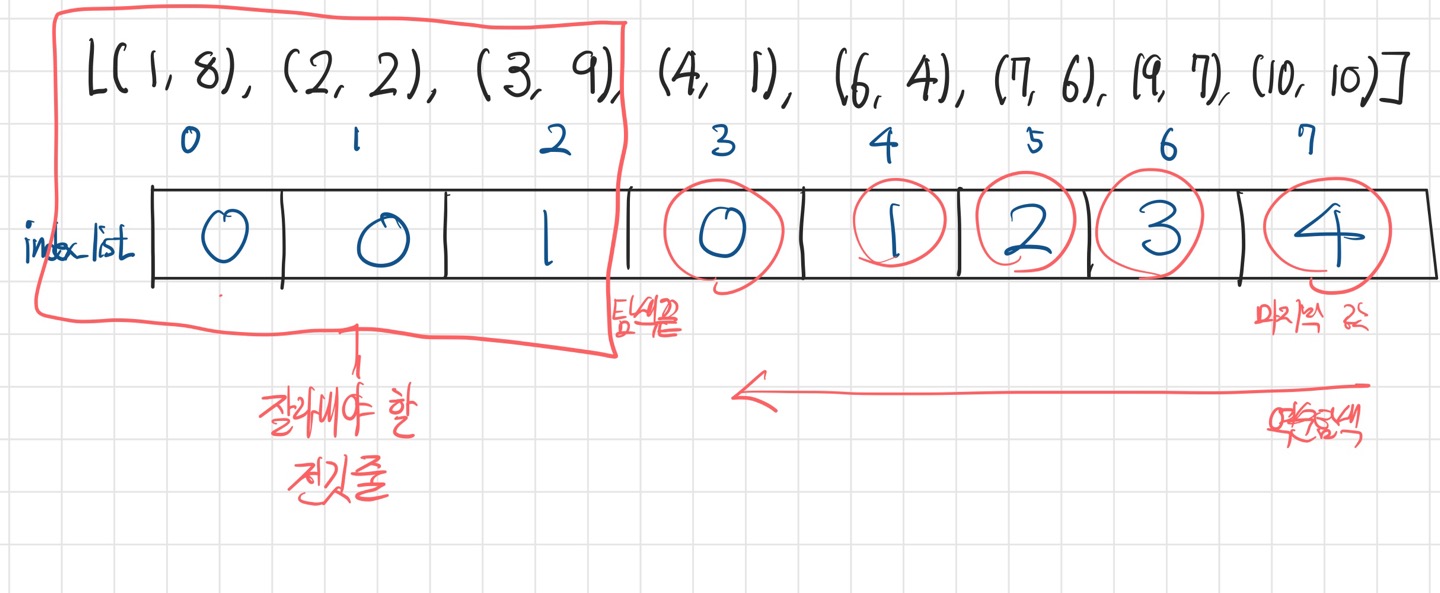
이제 index_list를 역순으로 탐색하며 실제 LIS를 구한다.
- LIS의 길이가 5이므로 LIS의 마지막 인덱스는 4일 것이다.
index_list[7] = 4이므로 7은 연결되어야 하는 전깃줄이다. - 탐색 값을 1 줄여서 3을 찾는다.
index_list[6] = 3이므로 6은 연결되어야 하는 전깃줄이다. - 이 과정을 탐색값이 0이 될때까지 반복한다.
- 위 그림에서 알 수 있듯이 0, 1, 2 인덱스가 잘라내어야 할 전깃줄이며, 여기에 대응되는
[1, 2, 3]을 답으로 출력하면 된다.
코드
완벽히 최적화된 풀이가 아닙니다. 참고만 해주세요…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import sys
input = sys.stdin.readline
def binary_search(num, right):
lo, hi = 0, right
while lo < hi:
mid = (lo + hi) // 2
if sorted_arr[mid][1] < num:
lo = mid + 1
else:
hi = mid
return hi
if __name__=="__main__":
N = int(input())
arr = [tuple(map(int, input().split())) for _ in range(N)]
arr.sort(key = lambda x : x[0])
sorted_arr = [] # 교차하지 않는 전기줄
index_list = [] # 로깅
sorted_arr.append(arr[0])
index_list.append(0)
count = 1
for i in range(1, N):
if sorted_arr[-1][1] < arr[i][1]:
sorted_arr.append(arr[i])
index_list.append(count)
count += 1
else:
idx = binary_search(arr[i][1], count)
sorted_arr[idx] = arr[i]
index_list.append(idx)
# 최장 증가 수열 길이 출력
print(N-count)
# 저장한 로깅 리스트를 거꾸로 탐색하며 꼬이지 않은 전깃줄 구하기
link_set = set() # 꼬이지 않은 전깃줄 번호 저장
find_idx = count - 1
for idx, inserted_idx in enumerate(index_list[::-1]):
if inserted_idx == find_idx:
link_set.add(N-idx-1)
find_idx -= 1
if find_idx < 0:
break
for i in range(N):
if i not in link_set:
print(arr[i][0])