Aivle Til 230208 데이터 처리 2

---

title: AIVLE TIL (‘23.02.08) - 데이터 처리 (2) date: 2023-02-08 12:49:05.451 +0000 categories: [에이블스쿨] tags: [‘aivle’] description: 데이터 분석을 위한 방법론, 분석을 위한 시각화 기법을 배워보자 image: /assets/posts/2023-02-08-aivle-til-230208-데이터-처리-2/thumbnail.png

---

오늘 배운 것

시계열 데이터 처리

시계열 데이터

• 시계열 데이터란
  1. 행과 행에 시간의 순서가 있고
  2. 행과 행의 시간 간격이 동일한 데이터를 말한다.

순서가 있다고 하여, Sequential Data라고도 한다.

• 일반 데이터에서 행은 그저 분석 단위로, 각 행은 서로 관련이 없다. 그러나 시계열 데이터에서는 행과 행에 시간의 순서라는 관련성이 있다.

datetime 변환

• csv 등으로 데이터셋을 불러왔을 때, 숫자로 변환할 수 없는 값들은 데이터프레임에서 모두 문자열 object로 저장된다.

• pd.to_datetime(df['Date']) 함수를 통해 변환 가능한 문자열 object를 datetime으로 변환할 수 있다.

• format= 옵션을 통해 파이썬에 어떤 것이 년/월/일인지 알려줄 수 있다.

  • Y : yyyy (2023) 형식의 년도
  • y : yy (23) 형식의 년도
  • m : 월
  • d : 일

date time에서 속성 추출

• datetime.dt.로 년, 월, 일, 요일 등 다양한 날짜 정보를 추출할 수 있다.

종류가 엄청 많다. 판다스 공식문서를 참고하자.

시계열 데이터 처리 메서드

아래의 메서드는 모두 시계열 데이터를 처리할 때만 사용하는 메서드이다.

Series.shift()

df['열이름'].shift(n)

• 시계열 데이터에서 시간의 흐름 전후로 데이터를 이동시킨다.
  • 양수 n = 해당 열의 값들을 n 행 뒤로 미룬다. 시계열 단위가 1일 일 경우 shift(3)이면 3일씩 밀려 현재 행에 3일 전 데이터가 오게 된다.
  • 음수 n = 해당 열의 값들을 n 행 앞으로 당긴다.
  • 기본값은 1이다.
• 사용 예시 : 오늘 판매량과 비교를 위해 같은 행에 전날 판매량 컬럼을 생성한다 -> shift()

Series.rolling()

df['열이름'].rolling(n).집계함수

• 현재 행부터 n행 전까지를 묶어서 집계한다.

• 3일 이동평균선 예시 : df['MA'] = df['price'].rolling(3).mean()

• min_periods 옵션 : 예를들어 rolling(3)의 경우 1행, 2행에서는 rolling에 들어갈 값이 부족해 값이 NaN이 된다. 하지만 min_periods = 1을 하면 최소 하나의 값으로도 집계가 가능해서 NaN이 생기지 않는다.

Series.diff()

`df[‘열이름’].diff(n)

• 차분이라고도 하며 현재 값과 n행 전 값의 차이를 구한다.

데이터분석 방법론

CRISP-DM

CRISP-DM은 한 번 수행하는 것으로 끝나는 것이 아니라, 계속 반복하는 사이클이다. 한 사이클을 완료한 시점에서 도메인과 데이터에 대해 더 많은 것을 알게되기 때문에 새로운 인사이트를 얻을 수 있다.

※ 파일럿 프로젝트 : 전체 프로젝트에 앞서 간결하고 축소된 형태의 프로젝트를 통해 전체 프로젝트의 가능성을 판단하는 프로젝트이다 (Go & Stop)

1. 비즈니스의 이해

   • 문제정의 : 해결하고자 하는 문제(target)를 정의하고, 평가지표를 선정한다.

   • 분석 목표

   • 초기 가설 수립 : 문제를 설명하는 요인(feature)를 선정한다. 초기 가설인 이유는 이후 추가 가설이 수립되거나 가설이 수정될 수 있기 때문

2. 데이터의 이해

   • 데이터 원본 식별 : 데이터의 원본이 어디에 있는지 확인한다. 이미 갖고있는 데이터와 현재 없지만 취득 가능한 데이터를 ‘가용한 데이터’라고 한다. 가용한 데이터를 한데 모아 분석 가능한 하나의 df로 만든다. 데이터 처리의 한 과정이다.

   • 데이터 탐색(EDA, CDA)을 통해 데이터셋을 분석하고, 가설을 검정한다.
     • 목적 : 가설 확인, 전처리 대상 정리, 데이터와 비즈니스를 더 잘 이해
     • 이해한 것을 통해 추가 가설 수립, 가설 수정 등을 할 수 있다.
   • 데이터 탐색 단계
     • 단변량 분석 : 개별 변수의 분포 분석
     • 이변량 분석1 : x와 y의 관계 분석 (가설의 검정)
     • 이변량 분석2 : x간의 독립관계 검정 ※ 최근의 트리 기반 알고리즘 등은 독립 여부가 중요하지 않아 중요성이 감소하는 추세
3. 데이터 전처리
   • 모델링을 위한 준비 단계이다.
     • 모든 셀에 값이 있어야 한다.
     • 모든 값은 숫자여야 한다.
     • 경우에 따라 값의 범위를 일치켜야 할 수 있다.
4. 모델링
5. 평가
   • 문제가 해결됐는지를 평가하는 단계이다.
6. 배포

데이터의 시각화

matplotlib과 seaborn을 통해 데이터프레임을 시각화 하는 것이 가능하다. 시각화를 구현하는 방법보다는 데이터에 맞도록 적절한 시각화를 선택하는 방법을 아는 것이 중요하다.

시각화의 목적

데이터의 단순 해석을 넘어 비즈니스의 인사이트를 파악하는 것

시각화의 한계

• 시각화는 결국 원본을 요약하는 것
• 요약을 하는 관점에 따라 해석의 결과가 달라질 수 있다.
• 어떤 식으로든 정보의 손실이 발생한다. (요약된 정보에서는 뭔가 놓칠 수 있다는 것을 항상 유념할 것)

단변량 분석

• 데이터의 특이점을 찾고 ‘왜 그렇지’라는 마음가짐으로 원인을 찾는 것이 중요하다.

숫자형 변수 요약

• 대표값을 통한 요약 : 평균, 중앙값, 사분위수 등 기초 통계량
  • 평균에는 산술평균, 기하평균, 조화평균 등이 있는데, 일단은 이러한 조율가 있다는 것 정도만 알자.
  • 평균의 함정을 조심하자.
  • df.describe를 통해 기초통계량을 한번에 요약하여 확인할 수 있다.
• 일정 구간마다의 빈도수 계산 : 도수분포표

숫자형 변수 시각화

• 기초 통계량 : Box plot

• 도수 분포표 : 히스토그램, KDE(커널 밀도 추정)

히스토그램

plt.hist(변수명, bins=구간 수) sns.histplot(x='변수명', data=df, bins = 구간 수)

x축은 시각화하고자 하는 정보, y축은 빈도수를 나타낸다.

히스토그램에서 제일 중요한 것은 구간수로, 구간수에 따라 플롯의 모양이 바뀔 수 있다.

정해진 정답은 없으며, 여러 구간 수를 보면서 적절히 해석 하는 것이 중요하다.

KDE Plot

모든 x값에 대해 데이터의 밀도를 추정한 플롯으로, 그래프의 넓이를 합하면 1이다.

a~b 구간의 넓이가 a~b 구간에 데이터가 존재할 확률을 나타낸다.

seaborn에서 kde=True 옵션을 통해 히스토드램과 KDE를 함께 표시할 수 있다.

Box Plot

plt.boxplot(변수명, vert) sns.boxplot(변수명)

• plt의 경우 데이터에 NaN이 포함되어 있다면 플롯이 출력되지 않는다.
• vert=는 박스플롯의 방향을 설정하는 옵션이다.
  • True(기본값) : 종으로 그린다.
  • False : 횡으로 그린다.
• seaborn에서는 vert옵션 없이 x= , y= 옵션을 통해 가능하다.

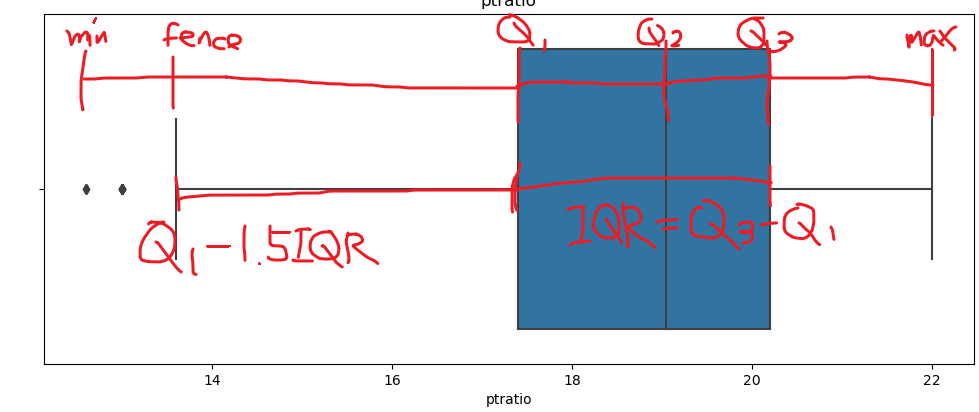
Box Plot 분석

파란색 상자는 Q1과 Q3 사이의 값을 나타낸다.

IQR은 이상치 후보를 추려내는데 사용하며 Q3 - Q1과 같다.

Box Plot에서는 펜스를 통해 이상치 후보를 찾아낸다. - 왼쪽 펜스는 Q1 - 1.5IQR과 데이터의 최소값중 더 큰 값 - 오른쪽 펜스는 Q3 + 1.5IQR과 데이터의 최대값중 더 작은 값

펜스를 벗어난 데이터는 이상치 후보가 되며 이상치 결정이 필요하다.

범주형 변수 요약

• 범주형 변수는 단순히 범주별 개수를 세면 된다.
  • 범주별 빈도수
  • 범주별 비율
• 범주별 빈도수를 토대로 Bar Plot을 그릴 수 있다.