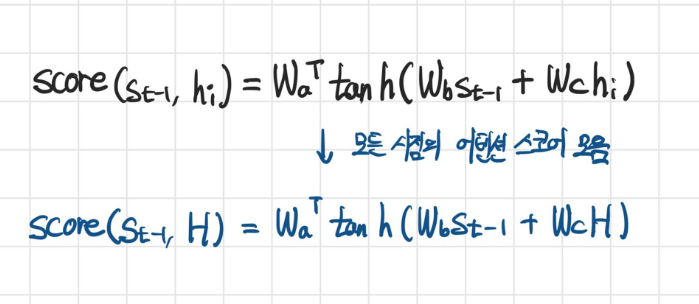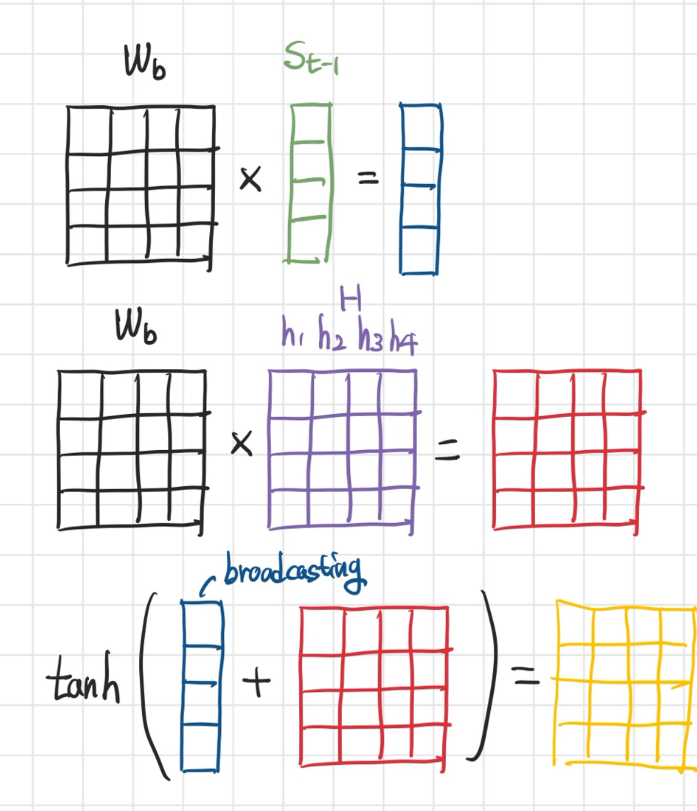Aivle Til 230401 언어지능 딥러닝 보충1
Aivle Til 230401 언어지능 딥러닝 보충1
title: AIVLE TIL (‘23.04.01) 언어지능 딥러닝 (보충1) date: 2023-04-01 09:15:18.008 +0000 categories: [에이블스쿨] tags: [‘aivle’] description: Attention 공부 image: /assets/posts/2023-04-01-aivle-til-230401-언어지능-딥러닝-보충1/thumbnail.png math: true —
서론
에이블스쿨 교육과정에서 시간 부족으로 인해 Attention에 대해 배우지 못했다. 또한, Attention 이후 transformer까지 배워보는 시간을 가져야 할 것 같아 보충 TIL을 작성하게 되었다.
딥 러닝을 이용한 자연어 처리 입문 교재를 참고하였다.
어텐션 메커니즘 (Attention Mechanism)
- RNN에 기반한 Seq2Seq 모델에는 크게 두 가지 문제점이 있다.
- 고정된 크기 벡터에 정보를 압축하는 과정에서 정보 손실이 발생
- RNN의 고질적인 문제인 기울기 소실(Vanising gradient)을 해결하지 못함
- 이로인해 입력 문장이 길 수록 번역 품질이 떨어지는 문제가 있다. 이를 해결하기 위해 어텐션이라는 기법이 등장하였다.
1. 어텐션의 아이디어
- 디코더의 출력 단어를 예측하는 매 시점마다 인코더의 전체 입력 문장을 참고한다.
- 그 중에서도 예측해야할 단어와 연관이 있는 입력단어를 더 집중(Attention)해서 보게된다.
2. 어텐션 함수
어텐션을 함수로 표현하면 다음과 같이 표현할 수 있다.
Attention(Q, K, V) = Attention Value
- Q = Query : t 시점에서 디코더 셀의 히든 스테이트
- K = Key : 모든 시점에서 인코더가 출력하는 각각의 히든스테이트
- V = Value : 모든 시점에서 인코더가 출력하는 각각의 히든스테이트
Key와 Value는 같은 값이며, Q와 K의 유사도를 구한 것을 Value에 곱해주어 Attention의 출력을 구한다.
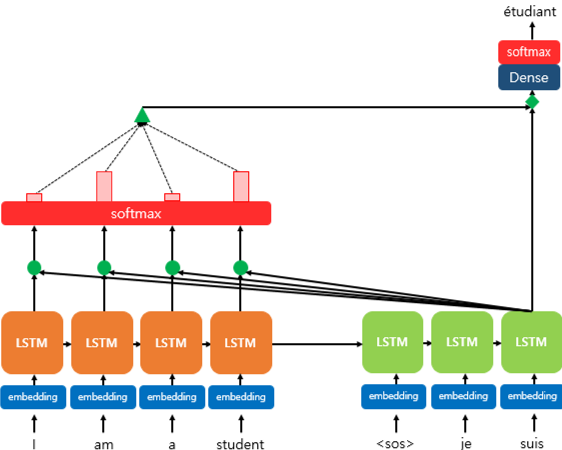
3. 닷-프로덕트 어텐션(Dot-Product Attention)
- t 시점에서 디코더가 다음 단어를 예측하기 위해 인코더의 모든 입력 문장을 참고하는 것이 어텐션이라고 하였다.
- 각각의 셀은 인풋 단어을 받아 히든 스테이트를 출력하는데, 모든 시점의 히든값에 대해 softmax함수를 거치면 각 인풋 단어가 디코더의 예측에 얼마나 도움이 되는지를 나타내는 확률값이 된다.
- 이 확률값을 하나의 정보로 담아 디코더로 전송하는데, 이를 통해 디코더는 어떤 인풋에 집중(Attention)하는지 알 수 있게되고, 더 정확하게 예측할 확률이 높아진다.
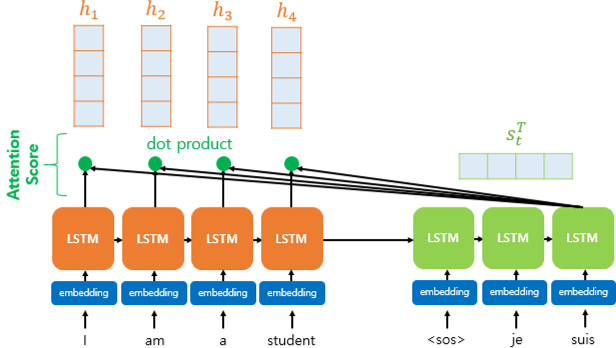
1) 어텐션 스코어 구하기
- 어텐션 스코어(Attention Score)는 인코더의 모든 히든 스테이트 값이 각각 디코더의 현재 시점의 히든 스테이트값과 얼마나 유사한지를 판단하는 점수이다.
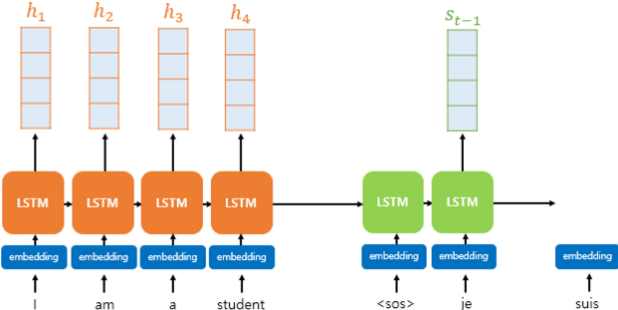
- 동일한 차원을 갖는 인코더의 히든스테이트 h와 디코더의 히든스테이트 s가 있다.
- t 시점의 디코더는 인풋으로 t-1 시점 디코더의 히든 스테이트와 t-1 시점 디코더의 출력 단어를 받는다.
- 어텐션에는 여기에 더해 어텐션 값(a)을 추가로 받는다.
- 이 어텐션 값을 구하기 위한 첫번째 과정이 바로 어텐션 스코어를 구하는 것이다.
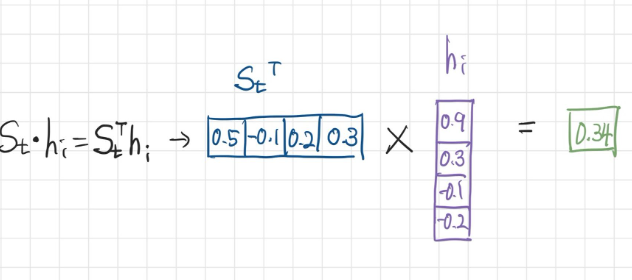
- 어텐션 스코어는 히든 스테이트 s와 h의 내적(dot produt)을 통해 구할 수 있다.
💡 내적은 두 행렬간의 유사도를 구하기 위해 사용할 수 있다! [1 1 1] · [1 1 1] = 3 [1 1 1] · [1 -1 1] = 1 [1 1 1] · [-1 -1 -1] = -3 두 행렬이 유사할 수록 내적은 큰 값을 갖고, 두 행렬이 다를 수록 작은 값을 갖는다.
- 이제 모든 인코더의 히든스테이트와의 어텐션 스코어를 구하여 모음값 e를 구한다.
2) 어텐션 분포(Attention Distribution) 구하기
- 어텐션 스코어 모음값 e에 softmax 함수를 적용하여 확률값으로 변환할 수 있다. 이렇게 변환된 값을 어텐션 분포라고 하며, 각각의 값을 어텐션 가중치라고 한다.
3) 어텐션 값(Attention Value) 구하기
- 각 어텐션 가중치와 히든 스테이트를 가중합하여 어텐션 함수의 최종 출력값인 어텐션 값 a를 구할 수 있다.
- 이렇게 구한 어텐션 값은 인코더의 문맥을 포함하고 있다고 하여 컨텍스트 벡터(context vector)라고도 한다.
4) 어텐션 값(a)과 디코더 히든 스테이트(s) 연결(Concate nate)
- a와 s를 연결하여 하나의 벡터(v)를 만들어낸다.
- 이 v를 예측값 연산에 입력으로 사용함으로써 모델의 성능을 상승시키는 것이 어텐션 메커니즘의 핵심이다.
5) 출력층의 Input 입력이 되는 s tilde 계산
- v에 대한 신경망 연산과 tanh 활성함수를 거침으로써 최종적으로 출력값의 인풋이 되는 s tilde를 계산한다.
- 신경망 연산에 사용되는 행렬은 학습이 가능한 가중치 행렬과 편향이다.
- s tilde를 출력층에 넣고 최종 신경만 연산을 함으로써 예측값 벡터를 얻어낸다.
4. 다양한 종류의 어텐션
- 위 예시에서는 내적을 바탕으로 어텐션 스코어를 구했지만, 보다 다양한 방법으로 어텐션 스코어를 구할 수 있다.
2. 바다나우 어텐션(Bahdanau Attention)
- 바다나우 어텐션은 어텐션 스코어를 구하는 과정에서 조금 더 복잡한 메커니즘을 사용한다.
1. 바다나우 어텐션 함수
- Attention(Q, K, V) = Attention Value
- Q = Query : t-1 시점에서 디코더 셀의 히든 스테이트
- K = Key : 모든 시점에서 인코더가 출력하는 각각의 히든스테이트
- V = Value : Query와 Key의 연산을 통해 구한 어텐션 스코어
- 쿼리값이 t시점이 아니라 t-1 시점임에 주의하자.
2. 바다나우 어텐션
- 마찬가지로 두 히든스테이트의 차원이 같다고 가정한다.
1. 어텐션 스코어 구하기
- 바다나우 어텐션에서는 어텐션 스코어를 계산하기 위해 또다른 학습가능한 가중치 행렬들을 사용해 신경망 연산을 한다.
- 연산 과정은 다음과 같다.
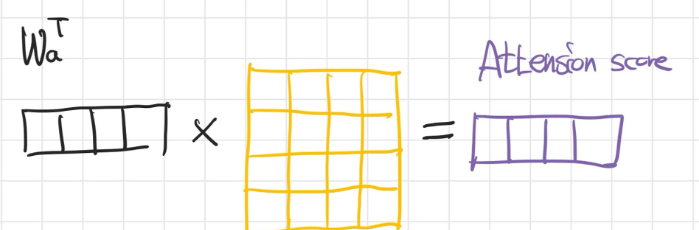
- \(tanh(W_{b}s_{t-1}+W_{c}H)\) 에서 두 행렬의 크기가 맞지 않으므로, broadcating으로 크기가 같도록 복제하여 연산한다.
- 최종적으로 구할 수 있는 어텐션 스코어는 각 시점의 인풋이 반영된 어텐션 스코어가 된다.
2) 어텐션 값 구하기
- 이후 어텐션 값을 구하는 과정은 닷-프로덕트 어텐션 값을 구하는 과정과 같다.
- 어텐션 스코어를 softmax 통해 확률값으로 변환
- 어텐션 스코어와 key(각 인코더 히든스테이트)의 가중합을 통해 어텐션 값을 구함
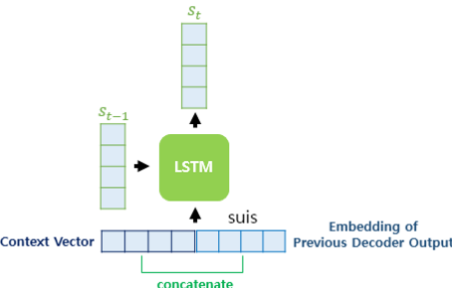
3) 어텐션 값을 통해 현재 시점의 히든 스테이트 값(s_{t}) 생성
- 닷-프로덕트 어텐션에서는 \(s_{t}\) 와 context vector를 concatenate하여 곧장 출력층의 Input으로 사용하였다.
- 바다나우 어텐션에서는 context vector를 t 시점의 디코더 Input과 concatenate를 한다. 그리고 이를 query(\(s_{t-1}\))와 신경망 연산하여 \(s_{t}\) 를 구한다.
- 이렇게 얻은 \(s_{t}\) 를 예측값 출력층의 Input으로 사용한다.
결론
- 매 디코더의 예측 시점마다 Encoder로 주어진 문맥을 확인할 수 있게 됨으로써 RNN의 근본적인 문제점인 Vanising gradient문제를 어느정도 극복하였다.
- 또한 그중에서도 제일 중요한 단어에 집중함으로써 더 높은 성능을 보일 수 있었다.
모델링
- 닷-프로덕트 어텐션 함수를 추가하여 모델링해보자
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 1. 세션 클리어
tf.keras.backend.clear_session()
# 2. 레이어 연결
# Encoder
enc_I = Input(shape=(kor_pad.shape[1],))
# Input을 이미 선언하여 shape를 지정해 주었으므로 input_length를 넣어줄 필요가 없음
enc_E = Embedding(kor_vocab_size, 128)(enc_I)
enc_S_full, enc_S = GRU(512, return_sequences=True, return_state=True)(enc_E)
# Decoder
# eos를 제외한 Input이 들어어오므로 -1
dec_I = Input(shape=(eng_pad.shape[1]-1, ))
dec_E = Embedding(eng_vocab_size, 128)(dec_I)
# 인코더의 마지막 시점 히든스테이트를 Input으로 받음
dec_H = GRU(512, return_sequences=True)(dec_E, initial_state=enc_S)
# Attention
key = enc_S_full # 인코더의 모든 히든스테이트
value = enc_S_full # 인코더의 모든 히든스테이트
query = dec_H # 디코더 각 시점의 히든스테이트
# 1. 어텐션 스코어(Attention Score) 구하기
score = tf.matmul(query, key, transpose_b=True)
# 2. 소프트맥스(softmax) 함수를 통해 어텐션 분포(Attention Distribution)를 구하기
# 마지막 축으로 소프트맥스 연산
att_dist = tf.nn.softmax(score, axis = -1)
# 3. 각 인코더의 어텐션 가중치와 은닉 상태를 가중합하여 어텐션 값(Attention Value)구하기
att_value = tf.matmul(att_dist, value)
# 4. 어텐션 값과 디코더의 t 시점의 은닉 상태를 연결(Concatenate)
dec_H = Concatenate()([dec_H, att_value])
# Fuclly Connected Layer
dec_H = Dense(512, activation='tanh')(dec_H)
# 아웃풋 레이어
dec_O = Dense(eng_vocab_size, activation='softmax')(dec_H)
model = tf.keras.models.Model([enc_I, dec_I], dec_O)
# 컴파일
model.compile(loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=['accuracy'],
optimizer='adam')
model.summary()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, 95)] 0 []
input_2 (InputLayer) [(None, 103)] 0 []
embedding (Embedding) (None, 95, 128) 1003776 ['input_1[0][0]']
embedding_1 (Embedding) (None, 103, 128) 394112 ['input_2[0][0]']
gru (GRU) [(None, 95, 512), 986112 ['embedding[0][0]']
(None, 512)]
gru_1 (GRU) (None, 103, 512) 986112 ['embedding_1[0][0]',
'gru[0][1]']
tf.linalg.matmul (TFOpLambda) (None, 103, 95) 0 ['gru_1[0][0]',
'gru[0][0]']
tf.nn.softmax (TFOpLambda) (None, 103, 95) 0 ['tf.linalg.matmul[0][0]']
tf.linalg.matmul_1 (TFOpLambda (None, 103, 512) 0 ['tf.nn.softmax[0][0]',
) 'gru[0][0]']
concatenate (Concatenate) (None, 103, 1024) 0 ['gru_1[0][0]',
'tf.linalg.matmul_1[0][0]']
dense (Dense) (None, 103, 512) 524800 ['concatenate[0][0]']
dense_1 (Dense) (None, 103, 3079) 1579527 ['dense[0][0]']
==================================================================================================
Total params: 5,474,439
Trainable params: 5,474,439
Non-trainable params: 0
__________________________________________________________________________________________________
- 어텐션 과정을 직접 계산하며 구현했지만 케라스가 제공하는 어텐션 레이어를 사용하는 것도 가능하다.
1
att_value = tf.keras.layers.Attention()([query, key])
This post is licensed under CC BY 4.0 by the author.