Aivle Til 230420 6차 미니프로젝트 정리

---

title: AIVLE TIL (‘23.04.20) 6차 미니프로젝트 정리 date: 2023-04-20 10:42:44.750 +0000 categories: [에이블스쿨] tags: [‘aivle’] description: 시계열 데이터를 다루어보는 프로젝트 image: /assets/posts/2023-04-20-aivle-til-230420-6차-미니프로젝트-정리/thumbnail.png

---

시계열 데이터 미니 프로젝트

프로젝트 개요

• 날씨 정보와 장애인 콜택시 이용 정보를 바탕으로 내일의 콜택시 대기시간을 예측하는 프로젝트

• 약 7~10년 치의 일별 시계열 데이터가 csv 형식으로 주어졌다.

프로젝트 목적

• 장애인 콜택시 이용 시 불편한 점을 조사한 결과 긴 대기시간에 가장 큰 불편함을 느끼는 것으로 조사되었다.
• 무작정 배차를 늘리는 것은 현실적으로 어렵기 때문에, 대기시간 예측 시스템을 제공함으로써 기다리는 동안 느끼는 불편함을 최소화하기 위해 머신러닝 모델을 이용하여 도착시간을 예측한다.

데이터 처리

컬럼별 데이터 분석

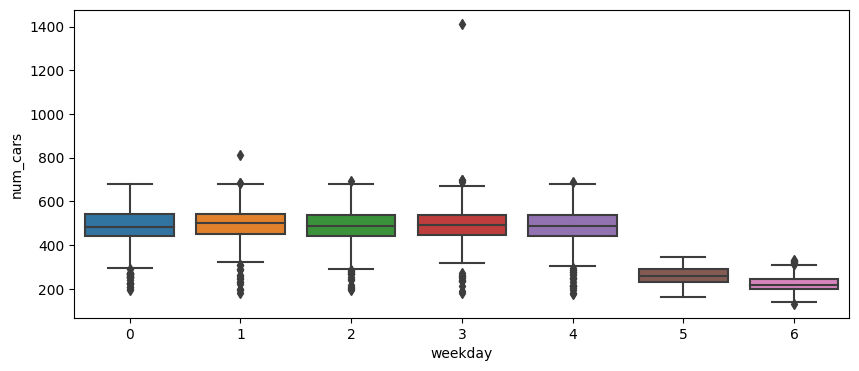
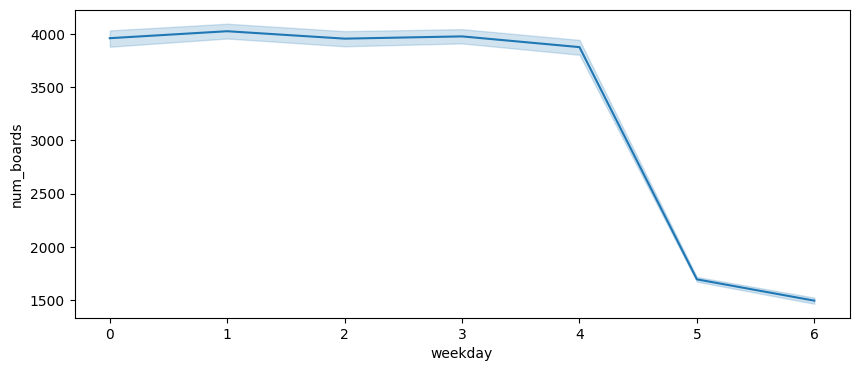
• 시계열 데이터인만큼 연도별, 월별, 요일별 등 시간대별로 EDA를 하는 것에 집중하였다.

• 전체적으로 그래프를 그려보았을 때 느낀점은 주중(월~금)과 주말(토, 일)의 데이터 차가 두드러진다는 것이다.
• 또한 주중에서 박스플롯을 그렸을 때 이상치 후보에 해당하는 데이터를 조회한 결과 높은 비율로 명절, 휴일이라는 것을 확인하였다. 때문에 주말과 휴일을 묶어 is_holiday라는 이진 범주 데이터로 분류하고자 하였다

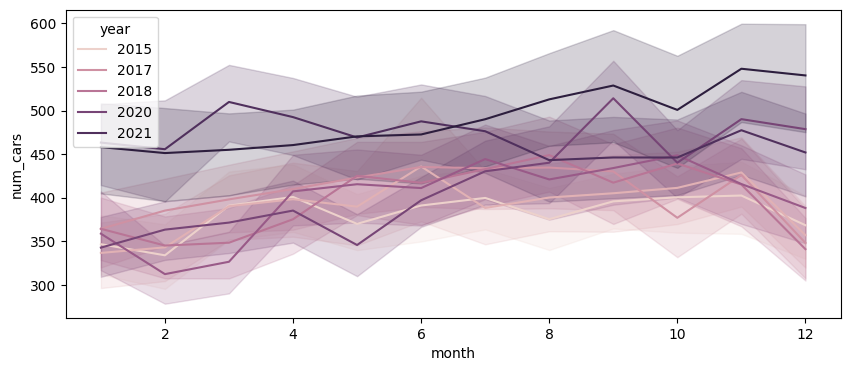
• 연도별로 살펴보았을 때는 시간이 흐름에 따라 평균적인 이용량이 증가하는 경향을 확인할 수 있었다.

특징 생성

휴일 여부

• 다소 부끄럽지만 휴일을 직접 입력하는 방식을 선택하였다.

• 그 이유는 첫째로 연도 범위가 7년으로 비교적 좁기 때문에 직접 입력하는데 걸리는 시간이 오래 걸리지 않는 다는 것이고, 둘째는 workalendar.asia가 대체 공휴일까지는 제공하지 않는다는 점이다. 때문에 대체 공유일까지 포함하여 직접 공휴일을 지정하는 방식을 택했다.

• 추가로 시계열에서 다른 데이터는 미래 데이터를 참고하는 것이 반칙에 해당하지만, 휴일인지 아닌지 여부는 미리 알 수 있고, 내일이 휴일인지 아닌지가 중요한 변수라고 생각하여 shift를 이용해 내일 휴일 여부를 변수로 사용하도록 하였다.

이동평균선

• 시계열 데이터 처리를 위한 가장 기초적인 통계량인 이동평균선을 추가하였다.
• 주중-주말이라는 요일별 요인이 크기때문에 7일간의 이동평균선을 추가하였고, 시간이 지날수록 전체적인 이용량이 증가하는 것을 고려해 30일간의 이동평균선도 추가하였다.

실제 탑승률

• 대기 시간이 길어질수록 신청은 하였지만 탑승하지 않는 비율이 높아짐을 확인할 수 있었다.
• 때문에 이용 신청 대비 실제 탑승률 특징을 생성하였다.

target 설정

• 하루 뒤의 대기 시간을 예측하는 것임으로 .shift(-1) 메서드를 이용하여 내일의 대기시간 데이터를 현재 행으로 가져왔다.

EDA

• 어떤 변수를 했는지를 모두 나열하는 것 보다는 인사이트를 얻었던 부분만 서술해보자.

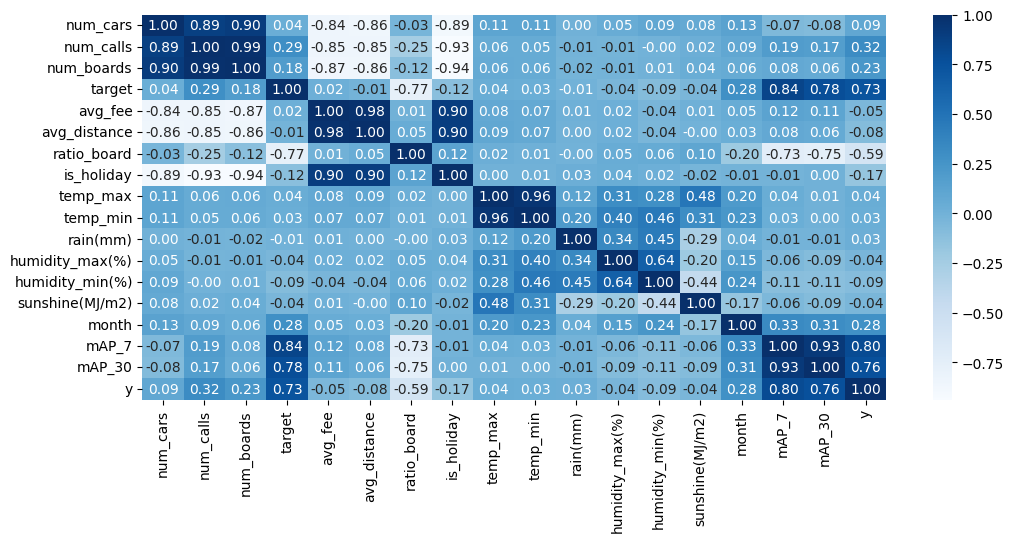
상관계수

• 가장 눈에 띄었던 것은 7일, 30일 이동 평균선이 전날의 이용자수(target)보다 y와의 상관계수가 더 높다는 것이었다. 아마 금->토와 같이 휴일 전후로 y값이 크게 바뀔때, 직전일의 데이터가 노이즈처럼 작용할 수 있을 것이라는 추측을 하였다.
• 또한 다른 데이터(ratio_board, num_calls)들이 충분히 target을 설명할 수 있는 변수라 생각하였기 때문에 다중공선성 제거를 위해 target 컬럼을 drop하기로 하였다.

시각화

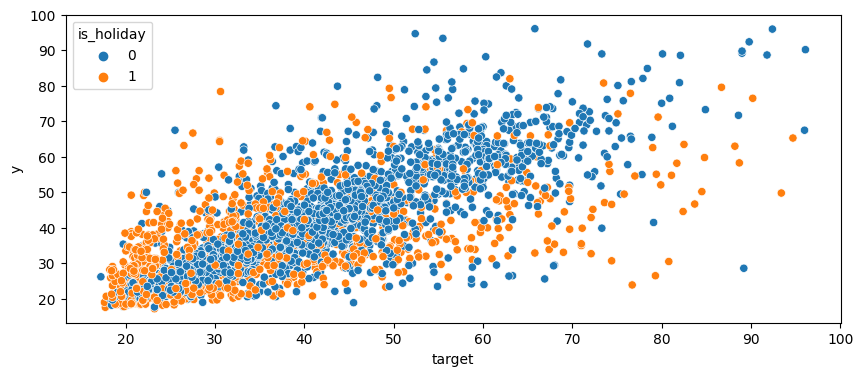
• 상관계수가 0.1 미만으로 높지 않았던 변수들도 시각화를 해보면 어느정도의 경향성을 보이는 경우가 많았다.
• 때문에 단순히 상관계수 수치로 판단하는 것 보다는 직접 시각화를 해보고 결정하는 것이 좋다는 것을 알게 되었다.

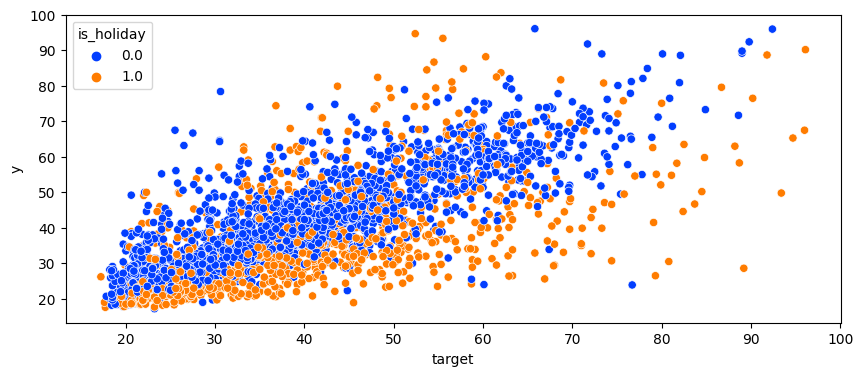
• 위 그래프는 is_holiday를 shift(-1)로 당기기전, 아래는 shift(-1)을 수행하고난 후이다. 확실히 y와의 관계성이 조금 더 뚜렷해 졌음을 확인할 수 있었다.

모델링

GRU를 이용한 딥러닝 모델

• RNN 기반 모델이 원래 시계열 데이터를 다루기 위해 나온만큼 반드시 RNN 기반 모델을 활용해 보겠다는 생각을 하였다.

데이터 전처리

• 시퀀스의 단어 하나하나가 시점 역할을 하는 자연어와 달리, Tabular 시계열 데이터를 그대로 모델에 넣으면 하루씩 모델에 반영되기 때문에 RNN 기반 모델을 쓰는 의미가 없어진다.
• 때문에 한번에 7개 시점을 고려하도록 하여 i~i+6일까지의 x데이터와 7일째의 y데이터가 데이터 하나가 되도록 numpy array를 만들어 주었다.

## 시계열 학습을 위해 데이터를 7일 단위로 잘라줌
# 예측할 시점
prediction_time_start = 7
prediction_time_end = y_train.shape[0]
# 입력 데이터와 타겟 데이터 구성
input_data = []
target_data = []
for prediction_time in range(prediction_time_start, prediction_time_end):
    input_data.append(x_train_sc[prediction_time-7:prediction_time])
    target_data.append(y_train[prediction_time])
    
input_data = np.array(input_data)
target_data = np.array(target_data)

input_data.shape, target_data.shape
>>>((2823, 7, 8), (2823,))

모델링

• 컬럼수가 많지 않고, 데이터 또한 적기 때문에 작은 모델을 만들었다.

# 세션 클리어
clear_session()
# 레이어 연결
il = Input(shape=(7, x_train_sc.shape[1]))
hl = GRU(256, return_sequences=True, dropout=0.2)(il)
hl = GRU(256, return_sequences=True, dropout=0.2)(hl)
hl = GRU(256, return_sequences=False, dropout=0.2)(hl)
hl = Dense(512, activation='swish')(hl)
hl = Dropout(0.2)(hl)
hl = Dense(256, activation='swish')(hl)
ol = Dense(1, activation='linear')(hl)
# 모델 선언
model_gru = Model(il, ol)
# 컴파일
model_gru.compile(loss=tf.keras.losses.MAE,
                    optimizer = optimizer)
# 요약
model_gru.summary()

모델 선정

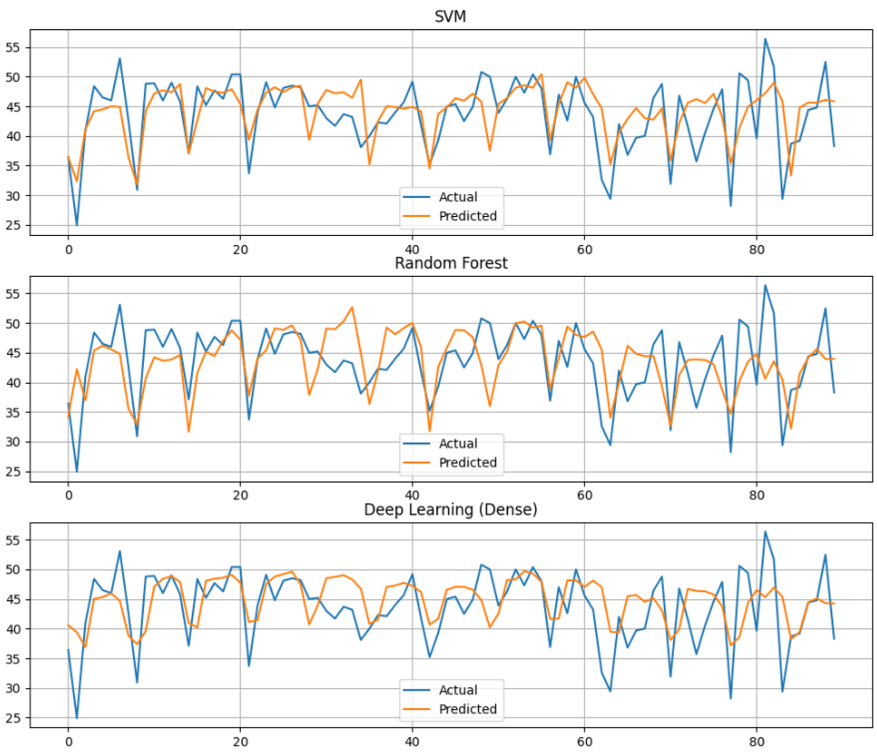
• 머신러닝 모델 3개, 딥러닝 모델 2개를 바탕으로 최종 모델을 선정하였다.

RF MAE: 4.337944444444444
RF MAPE: 0.10497016004449432

LGBM MAE: 4.698064907257304
LGBM MAPE: 0.1152820555856439

SVM(rbf) MAE: 3.920023449465459
SVM(rbf) MAPE: 0.09651161968948858

Deep Learning val_loss (Dense) : 4.5102
Deep Learning val_loss (GRU) : 4.9285

• 아무래도 데이터 수가 적어서 그런지 딥러닝 모델이 머신러닝 모델에 비해 떨어지는 성능을 보였다.
• 의외로 SVM 모델에서 제일 높은 성능을 내어 최종 선택하였다.

특징 선정

• 최초로 선정한 변수 외에도 이런 저런 변수를 더하고 빼가면서 성능이 어떻게 변하는지를 관찰하였다.

1. 기존에 제거했던 target 변수를 다시 추가

RF MAE: 4.500879120879121
RF MAPE: 0.11081339353997685

LGBM MAE: 4.751442426973392
LGBM MAPE: 0.11700754955505734

SVM(rbf) MAE: 4.386472626901607
SVM(rbf) MAPE: 0.10940582338268688

Deep Learning val_loss (Dense) : 4.4669
Deep Learning val_loss (GRU) : 4.7615

• 머신러닝의 경우에는 대체로 성능이 감소하였다. 즉 데이터간 공선성이나 노이즈가 있는 특징은 머신러닝에 안좋은 영향을 준다는 것을 확인할 수 있었다.
• 딥러닝의 경우 충분한 학습이 이루어지면 feature representation이 되기 때문에 소폭 증가했음을 확인할 수 있었다.

2. 중복 데이터만 제거하고 상관관계가 약한 변수를 전부 추가

RF MAE: 4.500076923076926
RF MAPE: 0.11236237866433593

LGBM MAE: 5.357368944198414
LGBM MAPE: 0.13343935153178763

SVM(rbf) MAE: 6.221996802160059
SVM(rbf) MAPE: 0.14353848727060758

Deep Learning val_loss (Dense) : 4.8564
Deep Learning val_loss (GRU) : 5.0761

• 딥러닝과 머신러닝 모두에서 성능이 감소하였다.

3. 모든 변수 사용

RF MAE: 4.6255714285714316
RF MAPE: 0.11378363789418271

LGBM MAE: 4.655814447958255
LGBM MAPE: 0.11492872789738516

SVM(rbf) MAE: 6.026767086401065
SVM(rbf) MAPE: 0.13962495237841524

Deep Learning val_loss (Dense) : 5.4655
Deep Learning val_loss (GRU) : 4.9922

• 2번 경우와 큰 차이가 없었다.

결론

• 주관적인 판단이긴 했지만 결국 처음에 정했던 변수 모음이 가장 좋은 성능을 내었다.
• 적어도 머신러닝에서는 중복 데이터 제거 및 약한 상관관계를 갖는 데이터 등을 찾아 제거하는 것이 모델 성능에 더 긍정적인 영향을 미친다고 생각한다.

하이퍼 파라미터 튜닝

optuna

optuna 공식 홈페이지

• 이전 게시글에서도 설명하였던 최적의 파라미터를 찾는 블랙박스 최적화 프로그램이다. 참조

# 1. 평가 결과를 반환하는 함수 작성
def objective(trial):
    # 하이퍼파라미터 탐색범위
    kernel = trial.suggest_categorical('kernel', ['rbf', 'linear'])
    gamma = trial.suggest_categorical('gamma', ['scale', 'auto'])
    cost = trial.suggest_float('C', 1e-1, 100, log=True)
    epsilon = trial.suggest_float('epsilon', 1e-2, 1, log=True)
    # 모델 선언

    model = SVR(kernel=kernel, gamma=gamma, C=cost, epsilon=epsilon)
    # 학습
    model.fit(x_train_sc, y_train)
    # 예측
    y_pred = model.predict(x_test_sc)

    return mean_absolute_error(y_test, y_pred)

# 2. 평가 결과를 받아 다음 파라미터값을 찾으며 최적의 하이퍼파라미터 탐색
study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100)

• 기본값 : SVM(rbf) MAE: 3.920023449465459

• 튜닝후 : SVM(rbf) MAE: 3.9135416323521373

• 미약하지만 성능이 증가한 것을 확인할 수 있었다.

결과 분석 및 특징 재선택

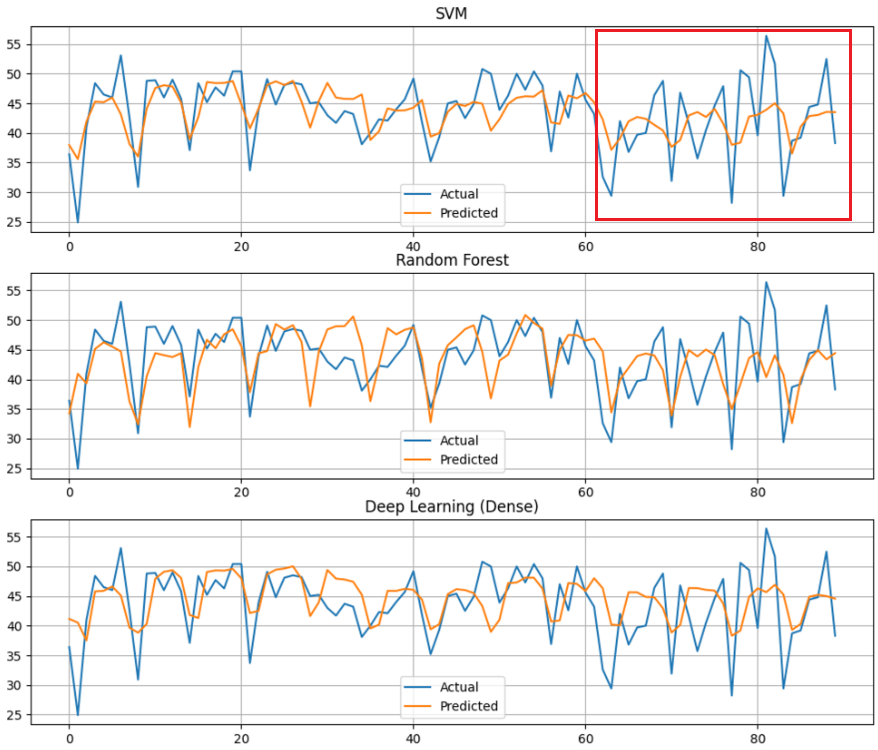
• 전체적으로 준수한 예측을 하였으나, 빨간색 네모칸 부분에서 예측이 많이 틀어지는 경향을 보였다.
• 이유를 생각해보니, 테스트 데이터는 10월~12월의 데이터이기 때문에 봄, 여름 및 대부분의 겨울 데이터는 하나도 예측에 사용되지 않는다는 것을 깨달았다.
• 때문에 범주형 데이터였던 계절 컬럼과 월별 컬럼을 전부 제거하였다.

SVM(rbf) MAE: 3.836902936672689

• 제거 후 MAE 오차도 감소하였고, 이전에 비해 겨울 데이터에 훨씬 더 정확한 예측을 하는 것을 확인할 수 있었다.

코멘트

좋았던 점

• 한동안 AutoML만 사용해서 모델을 다루는 실력이 퇴보하고 있다고 생각했는데, 오랜만에 직접 모델링과 튜닝을 수행하여 배운 것을 다시 점검해보는 시간이 되었다.

• 특징 선택에 대한 많은 인사이트를 얻을 수 있었다.

아쉬운 점

• 시간 부족으로 ARIMA 모델을 전혀 사용해보지 못한것이 아쉽다. 기회가 되면 공부해서 직접 사용해보자