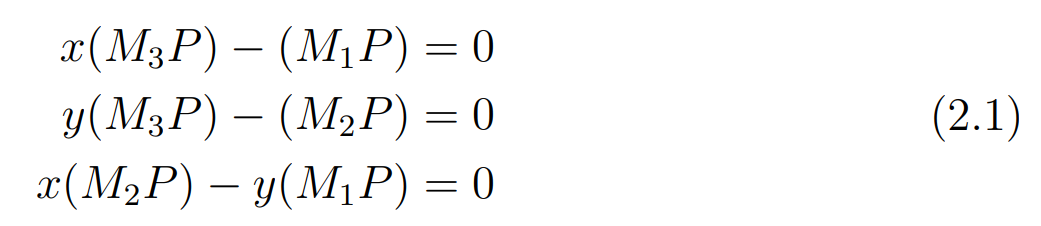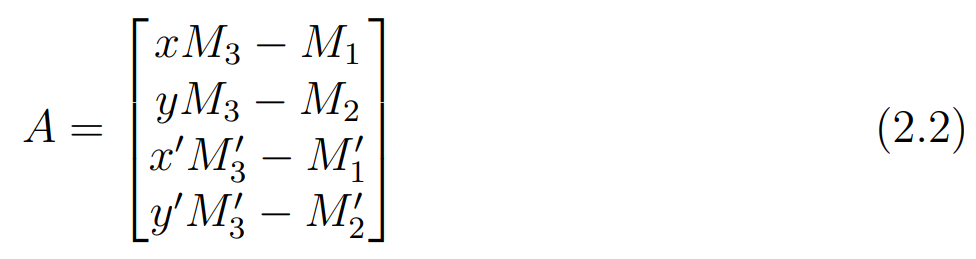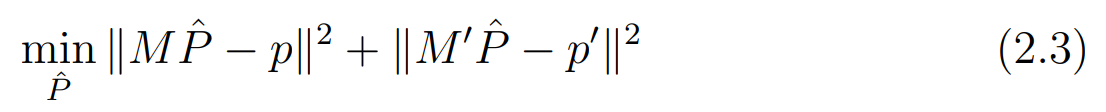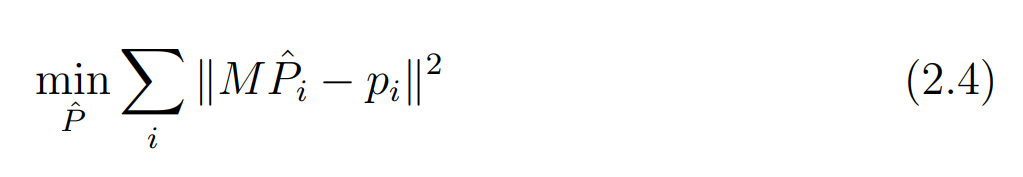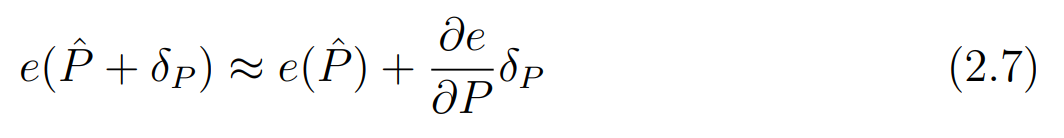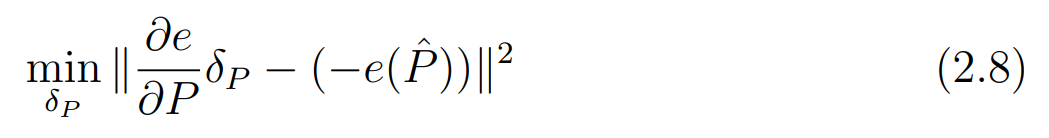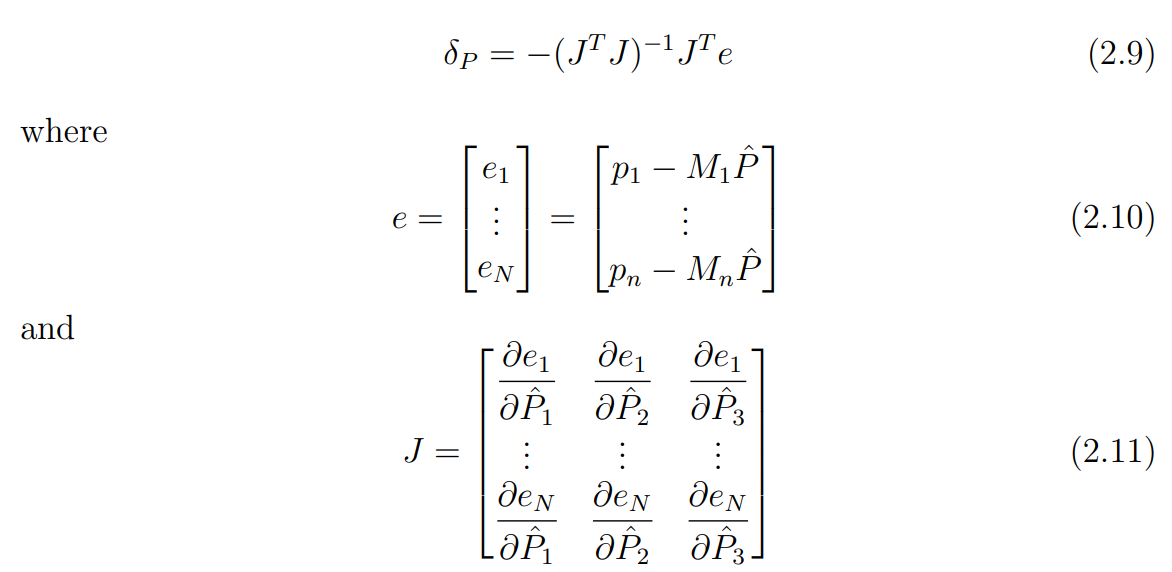CS231A 강의 노트 4 - stereo systems
스탠포드 3D CV 강의 CS231A 내용을 이해하는 것을 목표로 정리해보는 글
1. Introduction
이전 강의 노트에서는 epipolar geometry를 통해 현실에서 하나의 3D point가 두 이미지 평면에서 각각 어떤 위치에 투영되는지의 관계를 나타낼 수 있다는 것을 배웠다. 즉, 3D 정보 없이도 두 이미지 평면간의 관계를 알아 낼 수 있다는 것이다. 이번 강의 노트에서는 이를 이용해 여러 장의 2D 이미지로부터 3D 정보를 복원하는 방법에 대해 다루고 있다.
2. Triangulation (삼각측량)
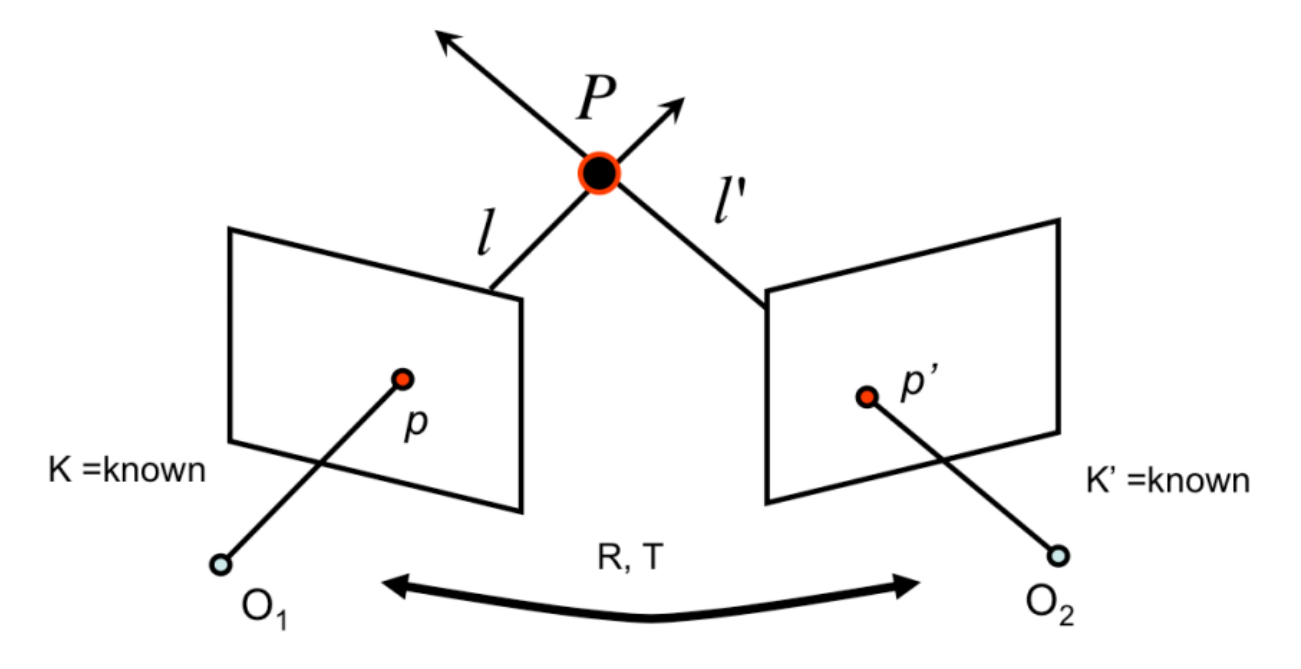
multiple view geometry에서 가장 기본적인 문제는 바로 triangulation(삼각측량)이다. 삼각측량은 말 그대로 동일한 3D point(\(P\))가 투영된 2장 이상의 이미지로부터 실제 \(P\) 의 위치를 복원하는 것이다.
이를 \(P\) 를 알기 위해서는 두 카메라의 intrinsic parameter(\(K, K'\)), 두 카메라간의 상대적인 회전 및 이동 정보(\(R, T\))가 필요하다. 카메라의 중심(\(O_1, O_2\))으로 부터 \(P\) 가 이미지 평면에 투영된 점 \(p, p'\) 를 향한 ray(\(l, l'\))를 쏠 경우, 이 ray는 한 점에서 교차하게 되며 이 점이 \(P\) 가 된다. 이를 통해 임의의 3D scene의 위치 정보를 좌표계로 나타낼 수 있게 된다. (3D 정보 복원)
이는 매우 간단해보이지만, 사실 현실에서는 카메라의 parameter 정보에는 오차가 있고, 투영된 점 \(p, p'\) 에도 오차가 발생할 수 있어 두 ray가 교차하지 않을 수 있다.
2.1 A linear method for triangulation
선형 방정식을 통해 두 ray가 교차하지 않는 문제를 해결해 볼 수 있다.
\(p\) 는 3D ponit \(P\) 가 카메라의 변환 행렬 \(M\) 에 의해 변환된 결과이므로 \(p, p'\) 를 각각 다음과 같이 정의할 수 있다.
\(p = MP = (x, y, 1)\) \(p' = M'P' = (x', y' 1)\)
동일한 벡터를 cross product하면 영벡터가 되므로 다음과 같은 제약식을 세울 수 있다.
\[p \times (MP) = [y(M_3P) - M_2P, M_1P - x(M_3P), x(M_2P) - y(M_1P)] = 0\]위 제약식을 이용하여 \(AP = 0\) 으로 만드는 어떠한 변환 행렬 \(A\) 를 다음과 같이 정의할 수 있다.
식 2.2는 두 카메라의 변환 행렬(\(M, M'\))과 투영된 점의 위치(\(p, p'\))만으로 A를 구할 수 있음을 나타내며, 이후로는 SVD를 통해 \(AP=0\) 이 되도록하는 최적의 \(P\) 를 찾는 linear estimate 문제를 통해 \(P\) 정보를 복원할 수 있다.
하지만 이 선형방정식을 이용한 방법은 projective-invariant(투영불변)하지 않다는 문제가 있다.
projective-invariant는 말 그대로 투영 변환에 대해 불변하다는 의미인데, 카메라의 변환 행렬 \(M\) 에서 투영 변환의 영향을 제거하기 위해 \(MH^{-1}\) 으로 식을 변경할 경우 아래와 같이 방정식이 바뀐다.
\[(AH^{-1})(HP) = 0\]SVD에서는 \(\|P\| = 1\) 이 되어야 하는데, P의 scale이 투영 변환 \(H\) 에 의해 변하게 되므로 투영 변환된 공간에 대해서는 적용할 수 없다.
즉 이 방법은 간단하지만, 대부분의 상황에서 적용할 수 없다는 문제가 있다.
2.2 A nonlinear method for triangulation
최적의 \(\hat{P}\) 를 찾는 문제를 다시 정의해보면, \(\hat{P}\) 를 이미지 평면에 재투영했을 때 \(p, p'\) 와의 거리(reprojection error)를 최소화하는 문제로 볼 수 있다. (식 2.3)
이미지가 2장 이상으로 늘어나도 단순히 각 이미지의 거리를 합하는 방식으로 적용이 가능하다. (식 2.4)
이 minimization 문제를 풀기 위한 세련된 접근법이 많이 존재하지만, 이번 강의 노트에서는 Gauss-Newton algorithm 하나만을 다룰 것이다.
일반적인 \(x \in \mathbb{R}^n\) 에 대한 nonlinear least squares problem은 다음과 같이 나타낼 수 있다.
\(r\) 은 \(r(x) = f(x) - y\) input \(x\) 를 사용한 function \(f\) 와, 관측값 \(y\) 와의 잔차를 계산하는 residual function이다.
함수 \(f\) 가 linear하다면 이 문제를 linear least square problem으로 간소화 할 수 있다. 그러나 일반적으로 homogeneous 좌표를 사용할 경우 \(p = (x, y, w)\) 와 같은 꼴이며 이를 이미지 좌표로 변환할 때 \(w\) 로 나누어주는 과정이 포함되므로 \(f\) 가 nonlinear이다. 즉, linear least square로 표현할 수 없다.
이러한 문제를 해결하기 위해 2 x 1 크기의 벡터 \(e_i = M\hat{P}_i - p_i = (\hat{x}-x, \hat{y} - y)^T\) 를 적용하여 최적화 문제를 다음과 같이 변경하여 나타낼 수 있다.
위 식 2.6이 최적의 3d point \(\hat{P}\) 를 찾기 위한 least squares problem을 완벽히 나타낸 표현이다.
이제 이 문제를 Gauss-Newton 알고리즘을 통해 어떻게 풀 수 있는지 알아볼 것이다. Gauss-Newton 알고리즘은 현재의 예측값(\(\hat{P}\))의 에러를 최소화 하는 쪽으로 보다 나은 예측값으로 업데이트 하는 것을 목표로 한다.
알고리즘의 각 스탭마다 \(\delta_P: \hat{P} = \hat{P} + \delta_P\) 의 업데이트가 발생한다. 여기서 중요한 것은 \(\delta_P\) 를 선택하는 것인데, Gauss-Newton 알고리즘의 핵심 아이디어는 현재의 예측값 \(\hat{P}\) 근처의 residual function의 선형 근사치를 찾는 것이다(linearize)
이 문제의 경우 오차를 미분하여 오차의 변화율을 구하는 것을 통해 오차를 선형적으로 근사하는 단계를 적용할 수 있다.
위 식을 통해 업데이트가 된 예측치의 오차를, 기존 예측치의 오차와 오차의 변화율 \(\times\) 변화량의 합으로 근사하였다.
이제 minimization proble을 다음과 같이 바꾸어 표현할 수 있다.
\[\underset{\delta_P}{min} \| e(\hat{P} + \delta_P) \|\]이렇게 잔차를 정의하는 것을 통해 standard linear least squeares problem으로 문제를 표현할 수 있다.
N개의 이미지에 대해, linear least squares solution은 다음과 같다.
사실 이부분을 전혀 이해하지 못했다.. Gauss-Newton Method에 대한 내용이라 이 부분은 별도로 공부하도록 하자.
결론적으로 e는 (N \(\times\) 1) 벡터이며, 이미지가 2개인 가장 단순한 경우에 e는 2 \(\times\) 1 벡터가 된다.
또한, \(\delta_P\) 를 계산하여 업데이트 하는 것을 \(e(\hat{P})\) 가 수렴할 때 까지 단순히 반복하는 것을 통해 \(\hat{P}\) 를 최적화 할 수 있다.
정리
이렇게 두 개 이상의 이미지로부터 3D 정보를 복원하는 방법에 대해 알아 보았다.
이 방법은 각 카메라의 intrinsic parameter와 카메라간의 상대적인 회전 및 이동을 알고 있을 때 적용할 수 있다.
하지만 실제로는 이 정보가 주어지지 않는 경우가 많다. 때문에 다음 게시글에서 다룰 강의 노트의 나머지 부분에서는 multi view 이미지로부터 3d scene의 구조와 camera parameter를 동시에 복원하는 structure from motion에 대해 배울 것이다.