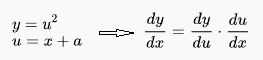Til 부스트코스 딥러닝 학습방법 이해하기 강의 정리

---

title: [TIL] 부스트코스 딥러닝 학습방법 이해하기 강의 정리 date: 2022-12-30 10:21:45.246 +0000 categories: [부스트코스-PreCourse] tags: [‘부스트코스’, ‘프리코스’] description: 데이터를 선형모델과 경사하강법을 이용해 해석하는 목적으ㄴ, 주어진 데이터의 정답인 y와 선형모델의 결과인 ŷ의 차이(L2-Norm)를 최소화하는 β를 찾는 것이다.하지만 복잡한 데이터나 분류가 필요한 데이터의 경우 선형모델만으로는 충분하지 않다.때문에 딥러닝에서는 선형 image: /assets/posts/2022-12-30-til-부스트코스-딥러닝-학습방법-이해하기-강의-정리/thumbnail.png

---

신경망 (neural network)

• 데이터를 선형모델과 경사하강법을 이용해 해석하는 목적으ㄴ, 주어진 데이터의 정답인 y와 선형모델의 결과인 ŷ의 차이(L2-Norm)를 최소화하는 β를 찾는 것이다.
• 하지만 복잡한 데이터나 분류가 필요한 데이터의 경우 선형모델만으로는 충분하지 않다.
• 때문에 딥러닝에서는 선형모델과 비선형 함수의 결합으로 이루어진 비선형모델인 신경망을 이용한다.

선형 모델

O = X * W * b O : 선형모델의 결과로 출력(output)되는 행렬 (행벡터 o_i를 원소로 가짐) - n x p X : 데이터 - n x d W : 일종의 연산자 역할을 하는 가중치 행렬 - d x p b : y절편에 해당하는 행벡터를 데이터의 개수(n)에 맞춰 모든 행에 복사한 행렬 n x p

• 입력 벡터(데이터)의 차원이 d에서 p로 바뀐다는 것을 기억하자

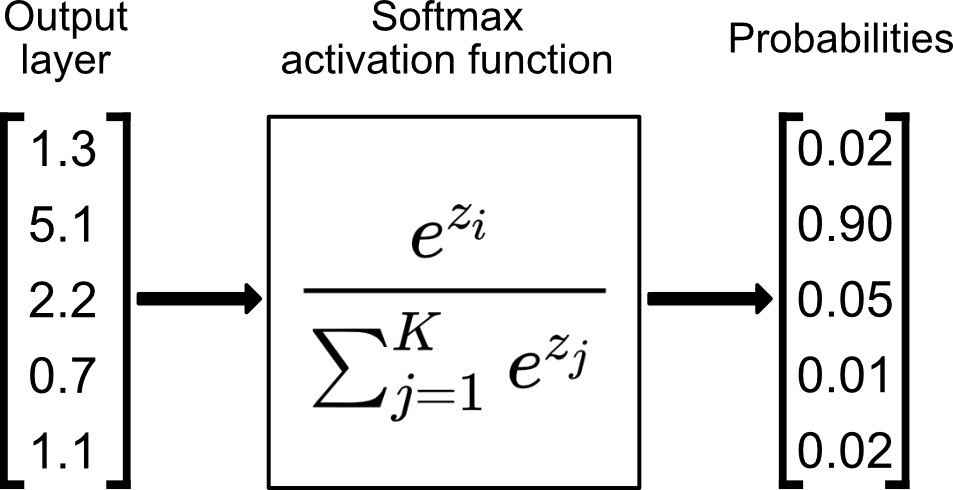
softmax(o) 함수

• softmax 함수는 출력벡터를 특정 클래스 k에 속할 확률을 나타내는 확률벡터로 변환하는 연산을 한다.
• 즉 모델의 출력을 확률로 해석할 수 있게 해준다.
• 분류 문제를 풀 때 주로 선형모델과 결합하여 사용한다.

출처 : https://towardsdatascience.com/softmax-activation-function-explained-a7e1bc3ad60

• softmax() 함수는 지수함수를 사용하여 구할 수 있다.

def softmax(vec):
	numerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
    # vec의 max값을 빼주는 이유는 지수함수이므로 값이 너무 커지면 overflow가 발생할 수 있기 때문이다. 
    # 분모, 분자가 동일한 값을 사용하므로 결과에 영향을 주지 않는다.
    denominator = np.sum(numerator, axis=-1, keepdims=True)
    val = numerator / denominator
    return val

softmax(O) = softmax(Wx + b)

• 추론 문제에서는 max(vec)의 값만을 1로 출력하는 원-핫(one-hot) 벡터를 사용하므로 softmax 함수를 사용하지 않는다.

신경망을 수식으로 나타내기

• 신경망은 선형모델과 활성함수(activation function)를 합성한 함수이다.

활성함수

• 선형모델의 출력물(O)에 대해, 각각의 원소에 개별로 적용되는 비선형(nonlinear) 함수
• 쉽게 말해 실수값을 input으로 받아 실수값을 출력하는 비선형 함수이다.
• 모든 원소를 고려하는 softmax와 달리, 한 원소에 대한 활성함수는 그 원소만 고려한다.

• 활성함수는 σ 기호로 나타낸다.

• 현재 딥러닝에서 가장 많이 쓰이는 활성함수는 ReLU 함수이다.
  • max{0, x} : 0보다 작으면 0, 0보다 크면 x를 출력한다.

잠재벡터

• 활성함수에 의해 변형된 벡터(신경망)를 말한다.
• Hidden vector라고 하며, H 기호로 나타낸다.

H = σ(z) = (σ(z₁), σ(z₂) … σ(z_n))

다층 퍼셉트론 (multi-layer Perceptron)

• 퍼셉트론은 다수의 입력값을 받아 하나의 결과(목적벡터)로 출력하는 알고리즘을 말한다.

X -> W(1), b(1) 과 σ(Z(1)) -> H (신경망 1개의 구조) H -> W(2), b(2) -> O (잠재벡터를 한 번 더 선형변환하여 출력) 이러한 구조를 2층 신경망이라 한다. 또한 이런 구조를 여러층 합성하여 만든 함수를 다층 퍼셉트론이라 한다.

• L층으로 이루어진 다층 퍼셉트론은 L개의 가중치 행렬(W)과 L개의 y절편 파라미터(b)로 이루어져 있다.

다층 퍼셉트론을 쓰는 이유

• 이론적으로는 2층 신경망만으로도 임의의 연속함수를 근사할 수 있다.
• 하지만 실전에서는 뉴런의 개수가 기하급수적으로 많아져 무리가 있다.
• 하지만, 층이 많을수록 목적함수 전사에 필요한 노드(뉴런)의 숫자가 빠르게 줄어든다.

• 결과적으로 조금 더 효율적인 학습이 가능하다.

• 하지만 무작정 층이 깊다고 좋은 것이 아니다.
• 층이 깊으면 근사는 쉽지만 최적화가 어려워진다는 단점이 있다.

순전파(foward propagation)

• 다층 퍼셉트론에서 l = 1, 2, 3 … L까지 순차적으로 신경망을 계산하는 것을 순전파라고 한다.
• 학습이 아니라 어떤 출력물을 출력하는 연산이다.

역전파(back propagation)

• 경사하강법을 적용하기 위한 알고리즘이다.
• 딥러닝은 역전파 알고리즘을 이용하여 각 층에 사용된 패러미터를 학습한다.
• 합성함수의 미분법인 연쇄법칙을 이용한다.
  • W(1) 을 편미분하기 위해 W(2)를 이용할 수 있다.
  • W(2) 를 편미분하기 위해 W(3)를 이용할 수 있다. …
  • 최종 목적지인 O를 이용할 수 있다.
  • 즉 저층에 있는 그래디언트 벡터를 계산할 때 위층의 그래디언트 벡터가 필요하다.
• 각 층의 그레디언트 벡터를 윗층부터 역순으로 계산한다.

해시넷 위키 링크

연쇄법칙 (chain-rule)

위 그림과 같이 y를 x에 대해 미분하기 위해 2번의 편미분을 순차적으로 이용하는 것이다.

• 이를 컴퓨터에 적용하기 위해서는 각 노드의 텐서 값을 기억해야 하므로 메모리를 많이 사용한다는 단점이 있다.