Til 부스트코스 부분공간의 기저와 차원 강의 정리

---

title: [TIL] 부스트코스 부분공간의 기저와 차원 강의 정리 date: 2023-01-11 05:58:04.563 +0000 categories: [부스트코스-PreCourse] tags: [‘부스트코스’, ‘프리코스’] description: 강의 주소 : https://www.boostcourse.org/ai251/lecture/540316?isDesc=false집합에서 어떤 전체집합의 부분집합을 subset이라고 한다.subspace는 선형 결합(linear combinations)에 대해 닫혀 image: /assets/posts/2023-01-11-til-부스트코스-부분공간의-기저와-차원-강의-정리/thumbnail.png

---

강의 주소 : https://www.boostcourse.org/ai251/lecture/540316?isDesc=false

Span and Subspace

Subspace의 정의

• 집합에서 어떤 전체집합의 부분집합을 subset이라고 한다.
• subspace는 선형 결합(linear combinations)에 대해 닫혀있는 subset이다. 이를 집합 H라는 기호로 표시한다.

닫혀있다(closed under)의 의미

• 집합에서 중복을 허용한 임의의 원소 조합으로 어떤 연산을 했을 때, 연산의 결과가 집합에 포함되어 있다면 그 집합은 해당 연산에 대해 닫혀있다고 한다.

• 다음과 같은 집합이 있다고 가정하자.
• 여기서 원소 2를 중복으로 뽑아서 곱하면 2 * 2 = 4의 결과가 나온다. 이를 집합에 포함시키자.
• 여기서 다시 원소를 뽑는다면 2 * 4 = 8, 4 * 4 = 16 등의 연산이 가능하다.
• 이를 무한히 반복하면 결국 집합 S는 2의 배수로 이루어진 무한한 집합이라는 것을 알 수있다.
• 이때 이 집합 S를 곱셈에 대해 닫혀있다고 한다.

subspace와 span의 관계

• subspace는 선형결합에 대해 닫혀있는 집합을 말한다.
• span은 재료벡터의 모든 선형결합 결과를 포함한다.
• 즉 subspace는 span과 유사한 개념이 되며, 모든 span은 subspace라고 할 수 있다.
• 반대로 말하면 어떤subspace H는 어떤 재료벡터들의 span으로 표현될 수 있다.

Basis of a Subspace

Basis(기저 벡터)의 정의

• 기저 벡터는 subspace H에서 두 가지 조건을 만족하는 벡터의 집합을 말한다.

1. H를 모두 덮을 수 있는 span의 (fully span) 재료 벡터여야 한다.
2. 기저 벡터의 성분끼리는 모두 선형 독립(linearly independent)이어야 한다.

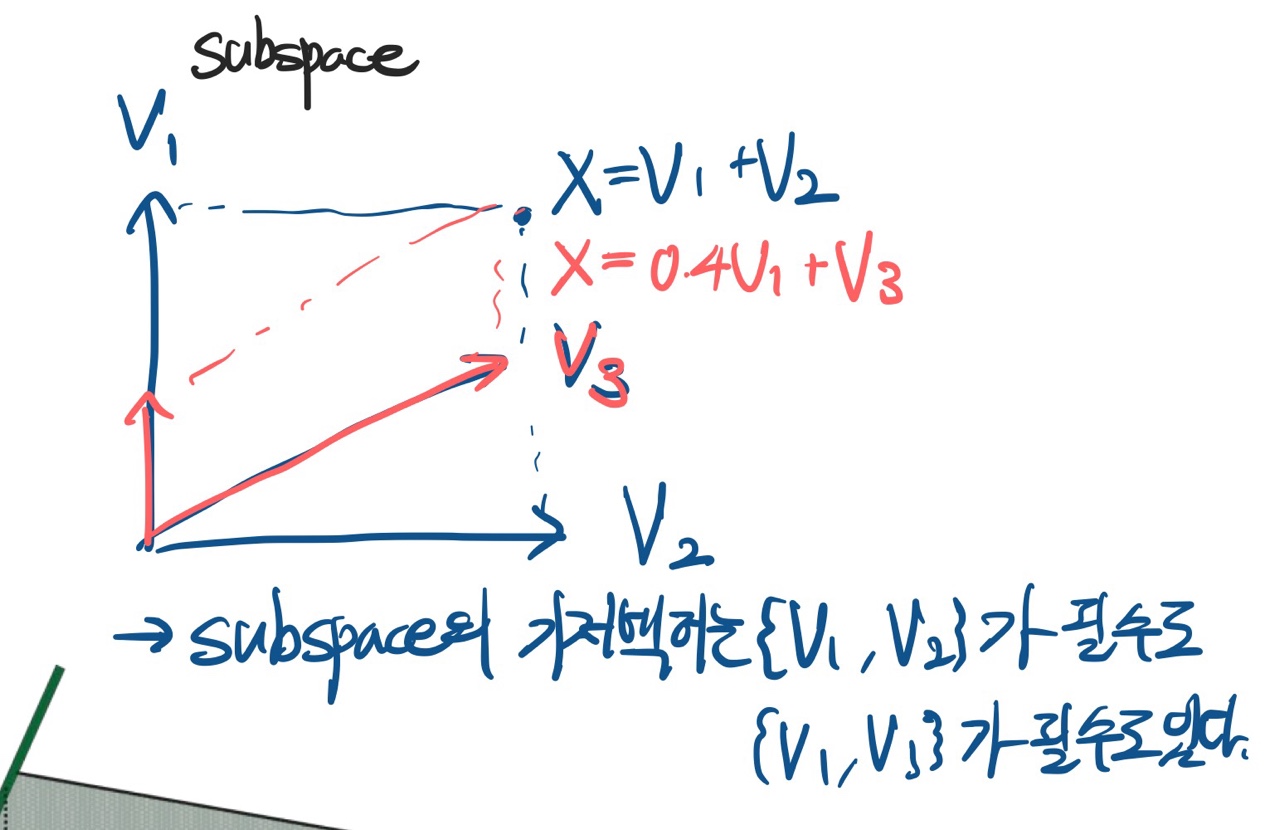
• 예를 들어 아래의 경우에서
• v3가 선형 의존이기 때문에 basis가 되지 못한다.
• {v1}은 H를 덮을 수 없기 때문에 마찬가지로 basis가 되지 못한다.
• {v1, v2}는 두 가지 조건을 모두 만족하므로 basis이다.

Non-Uniqueness of Basis

• subspace H에 대한 기저벡터는 여러개가 될 수 있다.

Subspace의 차원

• subspace에서 유니크한 요소는 바로 subspace의 차원이다.

Dimension of Subspace 정의

• subspace H에 대한 basis의 벡터 수를 H의 차원(dim H)이라고 한다.
• 어떤 basis도 벡터의 수는 동일하기 때문에 dim H는 하나의 값만 존재한다.

• 이 경우에서 dim H는 2이다.

Column Space

• 어떤 행렬 A에 대해 각각의 열벡터를 재료 벡터로 하여 만든 span을 A의 column space 또는 Col A라고 한다.

• 이 경우 dim Col A = 3이다.

선형 의존 관계에서 Column Space

• 각각의 열벡터가 선형 의존 관계라면, 해당 벡터를 추가하여도 Span이 늘어나지 않기 때문에 column space에서는 제외된다.

• 이 경우 dim Col A = 2이다.

Rank of Mattix

Rank의 정의

• 행렬 A의 rank는 column space의 차원을 의미한다.

Rank의 의의

• column 100개로 구성된 행렬 A가 있다고 하자.
• 만약 Rank A = 5라면 5개 column의 선형결합 만으로 나머지 95개의 column을 표현할 수 있다는 것을 의미한다.
• 즉 학습에서 데이터의 feature는 많지만, 대부분은 아무런 정보를 주지 못하는 쓸모 없는 feature임을 의미한다.
• 이 경우 몇개의 feature에만 계수가 좌지우지 되기 때문에 학습이 잘 이루어지지 않게 된다.